Обратная функция. Понятие сложной функции, явной и неявной функции.

Обратная функция. Если некоторая функция g в каждой точке х области значений обратимой функции f принимает значение у такое, что f(y) = x, то говорят, что функция g – есть обратная функция к f.

Если у нас будет задан график некоторой обратимой функции f, то для того чтобы построить график обратной функции, можно пользоваться следующим утверждением: график функции f и обратной к ней функции g будут симметричны относительно прямой, заданной уравнением y = x.

Если функция g является обратной к функции f, то функция g будет являться обратимой функцией. А функция f будет обратной к функции g. Обычно говорят, что две функции f и g взаимно обратные друг к другу.

Если функция y зависит от переменно u, т.е. , u Є U, а u, в свою очередь, является какой - либо функцией от независимой переменной х, т.е. , х Є Х, то переменная y называется функцией от функции (или сложной функцией) от ч и записывается в виде .

Область определения сложной функции - это множество тех значений х Є Х, для которых функция g(x) определена, кроме того, значения u принадлежат области определения функции y = f(u).

Переменную u принято называть промежуточным аргументом в отличие от независимой переменной х.

Явной функцией от переменной называется функция вида: y = f(x), такая, что можно явным образом выразить через зависящую переменную.

Неявной функцией от двух переменных называется функция вида F(x,y)=0, когда мы не можем выразить явным образом одну из переменных функции с помощью другой переменной.

Явная функция у(х) задается формулой вида y = f(x), т.е. значение у вычисляется просто

подстановкой х. Например, 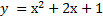. Неявная функция у(х) задается уравнением вида f(x,y)=0, т.е. для вычисления ее значения надо решать уравнение. Например, уравнение задает ДВЕ неявные функции:

и 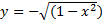. Это же уравнение можно рассматривать и как задание неявной функции х(у).

Не нашли, что искали? Воспользуйтесь поиском: