ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производные и дифференциалы высших порядков.
1. Производные и дифференциалы высших порядков
Опр-ие: производной 2-го порядка функции у=f(х) называется производная (первого порядка) от производной (n-1)-го порядка. f''(x)=(f'(x))'
- общая формула
Опр-ие: Дифференциалом n-го порядка функции у=f(х) называется дифференциал первого порядка от дифференциала (n-1)-го порядка.
- общая формула
Основные свойства производных и дифференциалов высших порядков:
1. Если С = конст, то 
2. 
3. Формула Лейбница
Формула Лейбница для n -ой производной произведения двух функций — обобщение правила дифференцирования произведения (и отношения) двух функций на случай n-кратного дифференцирования.
Пусть существуют функции u = u(x) и v = v(x), имеющие производные до n-ного порядка включительно.
Тогда 
, где 
- число сочетаний из n по k
4. Бином Ньютона
формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
, n - неотрицательное целое число, a и b - переменные.
Теорема Ферма.
Если функция y = f(x) непрерывна и дифференцируема на [a, b], и внутри этого интервала достигает наибольшего или наименьшего значения в т.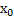 
, то первая производная в т. 
.
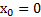Теорема Ролля.
Если фукция y = f(x) непрерывна и дифференцируема на [a, b] и принимает равные значения на концах [a, b] (f(a) = f(b)), то по-крайней мере в одной внутренней точке эпсилон, которая больше a, но меньше b (a<E<b), 
, 
Теорема Лагранжа.
Если функция y = f(x) непрерывна и дифференцируема на [a, b], то внутри [a, b] есть хотя бы одна точка эпсилон, для которой выполняется условие:
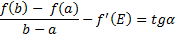
Не нашли, что искали? Воспользуйтесь поиском: