Необходимые и достаточные условия существования точек перегиба функции.

Достаточные условия наличия точки перегиба.

Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке 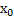. Если f '' (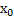) меняет знак при переходе через точку 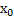, то – то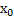чка перегиба функции f (x).

Если f '' (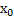) = 0, , то – точка перегиба функции f (x)

Выпуклость и вогнутость графика функции в точке (аналитический признак)

План исследования и построения графиков функций.

1. Определение области определения функции.

2. Нахождение четности (нечетности) функции

3. Нахождение корней функции (точки пересечения с осью х) с осью у.

4. Нахождение точек разрыва функции и их исследование.

5. Определение характера функции на концах области определения.

6. Нахождение вертикальные, горизонтальные, наклонные асимптоты (если они есть).

7. Исследование функции по первой производной (найти интервалы, монотонности, убывание, возрастание, экстремумы)

8. Исследование функции по второй производной.

35. Первообразная функции. Неопределенный интеграл и его функции(может свойства?? нужно правила интегрирования?).

F(x) - первообразная функция называется первообразной от функции f(x) на [a, b], если на этом интервале выполняется равенство f'(x) = f(x), т.е. первообразная - это функция, которая будучи продифференцированная, дает подынтегральную функцию f(x).

, где

- подынтегральное выражение

- подынтегральная функция

- дифференциал независимой переменной

С - константа интегрирования в неопределенном интеграле.

Множество F(x) + C всех первообразных функций для данной функции f (x), где C принимает все возможные числовые значения, называется неопределенным интегралом от функции f (x) и обозначается символом .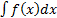

Нахождение первообразной относительно подынтегральной функции называется процессом нахождения неопределенного интеграла (интегрированием)

Интегрирование - процесс обратный дифференцированию.

Свойства неопределенного интеграла:

1. 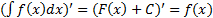- производная от некоторого интеграла - подынтеграл функции.

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

3. Неопределенный интеграл от дифференциала функции равен этой функции + произвольная постоянная (С)

Таблица неопределенных интегралов от основных элементарных функций.

37. Методы интегрирования: замена переменной, интегрирование по частям.

Метод замены переменной (метод подстановки).

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

Пусть требуется вычислить интеграл . Сделаем подстановку , где — функция, имеющая непрерывную производную.

Тогда . Теперь полученные выражения подставим в интеграл и получим:

Интегрирование по частям:

Интегрирование по частям — применение следующей формулы для интегрирования:

При использовании формулы интегрирования по частям, надо разбить подынтеграл выражения на u и dv так, чтобы второй интеграл был проще первого.

Не нашли, что искали? Воспользуйтесь поиском: