ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Интегрирование простейших рациональных дробей.
Метод заключается в разложении рациональной дроби на сумму простейших дробей.
- многочлен с действительными числами
Дробь считается неправильной, если старшая степень числителя больше, либо равно старшей степени знаменателя.
1) 
- выделили правильную дробь
- целая часть от 
- правильная дробь
2) Правильную дробь разлагают на простые множители, для этого находим корни уравнения.
Q(x) = 0 - разлагаем на множители 1-ой и 2-ой степени с действительными коэффициентами.
39. Интегрирование тригонометрических функций (нужно ли рассматривать частные подстановки?).
Интеграл вида 
с помощью "универсальной тригонометрической подстановки" 
сводится к интегралу от рациональной функции, при этом
и 
, также
,
Частные подстановки:
1. 
, это взяли из формулы 
.
2. Если sinx и cosx в интеграле только в четных степенях, то используем подстановку 
3. Если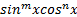 
, где m, n - нечетная степень, то принимаем любую функцию за t:
t = sinx или t = cosx
40. Определенный интеграл: определение, свойства, геометрический смысл.
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 
) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись 
.
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Свойства определенного интеграла:
1) Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
.
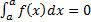Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:
.
2) Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е. 
3) Постоянный множитель можно выносить за знак определённого интеграла, т.е.
4) Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
5) При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
Геометрический смысл: с помощью определенного интеграла можно вычислять площади фигур, а при известных поперечных сечениях трехмерных тел – их объемы.
41. Вычисление определенного интеграла: формула Ньютона-Лейбница(Что тут еще нужно?).
Для вычисления определенного интеграла от непрерывной функции надо найти для нее первообразную функцию и составить разность значений этой последней функции при верхнем и нижнем пределах интегрирования.
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a, b], то
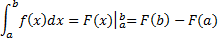
Не нашли, что искали? Воспользуйтесь поиском: