Свойства линейно зависимых и линейно независимых векторов 1 страница

Замечания 1.2

1. Один вектор тоже образует систему: при — линейно зависимую, а при — линейно независимую.

2. Любая часть системы векторов называется подсистемой.

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.

4. Система из векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов линейно независима, а после присоединения к ней вектора 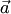оказывается линейно зависимой, то вектор 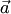можно разложить по векторам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

13. Предложение о разложении в зависимой системе одного вектора через другие.

Докажем, например, последнее свойство. Так как система векторов — линейно зависима, то существуют числа 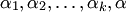, не все равные 0, что. В этом равенстве . В самом деле, если , то . Значит, нетривиальная линейная комбинация векторов равна нулевому вектору, что противоречит линейной независимости системы . Следовательно, и тогда , т.е. вектор 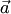есть линейная комбинация векторов . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения и , причем не все коэффициенты разложений соответственно равны между собой (например, ).

Тогда из равенства 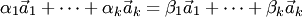получаем .

Следовательно, линейная комбинация векторов равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов . Полученное противоречие подтверждает единственность разложения.

14. Теорема о зависимых системах в разных пространствах.

Пусть r – ранг матрицы А порядка p на n, . Пусть М – базисный минор матрицы А. Все строки (все столбцы) матрицы А, которые не участвуют в образовании базисного минора М, линейно выражаются через строки (столбцы) матрицы, порождающие базисный минор М.

А теперь поясним связь теоремы о ранге матрицы с исследованием системы векторов на линейную зависимость.

Составим матрицу A, строками которой будут векторы исследуемой системы :

Что будет означать линейная независимость системы векторов ?

Из четвертого свойства линейной независимости системы векторов мы знаем, что ни один из векторов системы не выражается через остальные. Иными словами, ни одна строка матрицы A не будет линейно выражаться через другие строки, следовательно,линейная независимость системы векторов будет равносильна условию Rank(A) = p.

Что же будет означать линейная зависимость системы векторов ?

Все очень просто: хотя бы одна строка матрицы A будет линейно выражаться через остальные, следовательно, линейная зависимость системы векторов будет равносильна условию Rank(A) < p.

Итак, задача исследования системы векторов на линейную зависимость сводится к задаче нахождения ранга матрицы, составленной из векторов этой системы.

Следует заметить, что при p > n система векторов будет линейно зависимой.

Замечание: при составлении матрицы А векторы системы можно брать не в качестве строк, а в качестве столбцов.

15. Разложение вектора по базису. Теорема о единственности разложения вектора в базис.

Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису. Пусть - базис n-мерного векторного пространства. Добавим к этим векторам n-мерный вектор x. Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где - некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.

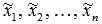Предположим, что существует еще одно разложение , где - некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :

Так как система базисных векторов линейно независима, то поопределению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.

16. Декартовый базис и декартовые координаты вектора. Теорема о разложении вектора в декартовый базис.

Рассмотрим декартову прямоугольную систему координат Oxyz. Обозначим , , – единичные векторы, направленные соответственно вдоль осей Ox, Oy, Oz (орты осей). Эти векторы называются декартовым прямоугольным базисом в пространстве.

Пусть – произвольный вектор в пространстве. Перенесем его начало в точку O ( ) и построим прямоугольный параллелепипед, в котором вектор является диагональю (рис. 11). Тогда , где , , – составляющие вектора по осям Ox, Oy, Oz. Но , аналогично ,

.

Рис. 11

Обозначая , , , получим .

Это равенство называется разложением вектора по базису , , , а числа , , называются координатами вектора в этом базисе, или декартовыми прямоугольными координатами вектора. Пишут или .

17. Длина вектора.

Зная координаты вектора, легко выразить его длину:

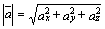(2.2)

(квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений).

Если , где , , то , , . Тогда , или

– (2.3)

так выражаются координаты вектора через координаты его начала и конца.

18. Линейные операции над векторами заданными своими координатами. Теорема о нахождении координат через две точки (без доказательства)

Пусть в декартовой системе координат на плоскости Oxy нам известны координаты точек начала и конца вектора : . Найдем координаты вектора .

Если вспомнить геометрическое определение операции сложения двух векторов, то можно записать равенство (О – начало координат), откуда находим .

Векторы и являются радиус-векторами точек А и В в заданной прямоугольной декартовой системе координат, следовательно, их координаты равны соответствующим координатам точек А и В, то есть, . Тогда, опираясь на теорию статьи операции над векторами в прямоугольной системе координат, находим .

Аналогично, в трехмерном пространстве для точек справедливо .

Таким образом, координаты вектора равны разности соответствующих координат точек его конца и начала, то есть, на плоскости , а в трехмерном пространстве .

19. Направляющие косинусы

Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где , ,  – углы, составляемые вектором с осями x, y, z соответственно.

Сумма квадратов направляющих косинусов равна 1.

20. Скалярное произведение векторов.

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид , где и - длины векторов и соответственно, а 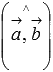- угол между векторами и .

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .

Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .

21. Основные понятия.

Решение различных задач на вычисление скалярного произведения векторов сводится к использованию свойств скалярного произведения и формул

1. ;

2. ;

3. или ;

4. .

22. Свойства скалярного произведения.

Свойства скалярного произведения:

1) ;

2) ;

3) ;

4) , или , или .

Таким образом, – условие перпендикулярности векторов.

5) , или, обозначая (скалярный квадрат вектора ), получим , откуда .

23. Теорема о необходимом и достаточном условии перпендикулярности векторов.

Для перпендикулярности двух ненулевых векторов и необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство .

Пусть векторы и перпендикулярны. Докажем выполнение равенства .

По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы и перпендикулярны, то угол между ними равен девяноста градусам, следовательно, , что и требовалось доказать.

Переходим ко второй части доказательства.

Теперь считаем, что . Докажем, что векторы и перпендикулярны.

Так как векторы и ненулевые, то из равенства следует, что . Таким образом, косинус угла между векторами и равен нулю, следовательно, угол равен , что указывает на перпендикулярность векторов и .

Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.

24. Выражение скалярного произведения двух векторов через координаты сомножителей.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов a и b.

То есть, для векторов 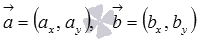на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид
, а для векторов в трехмерном пространстве скалярное произведение в координатах находится как
.

25. Угол между векторами, условие параллельности и перпендикулярности двух векторов.

Углом между векторами a и b называется угол между лучами OA и OB.

Векторы a и b называются перпендикулярными, если угол между ними равен 90 ( радиан). Косинус угла между векторами и , а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах и .

Разберем эти случаи.

По определению скалярное произведение векторов есть . Если векторы a и b ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов a и b, и мы получим формулу для нахождения косинуса угла между ненулевыми векторами: . Эту формулу можно использовать, если известны длины векторов и их скалярное произведение.

26. Физический смысл скалярного произведения.

Скалярным произведением двух векторов (обозначается или 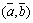) называется число, равное произведению длин этих векторов на косинус угла между ними: , где .

Учитывая, что , , можно записать: . Отсюда

. (2.8)

Из физики известно: если – постоянная сила, действующая на материальную точку, а – вектор перемещения точки под действием этой силы, то работа, совершаемая силой на участке l, равна .

27. Векторное произведение векторов

28. Основные понятия

Векторным произведением двух векторов a и b, заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор c, что

- он является нулевым, если векторы a и b коллинеарны;

- он перпендикулярен и вектору a и вектору b ();

- его длина равна произведению длин векторов a и b на синус угла между ними ();

- тройка векторов a,b,c ориентирована так же, как и заданная система координат.

29. Геометрический смысл

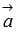По определению длина векторного произведения векторов равна . А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы и 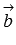, если их отложить от одной точки. Другими словами, длина векторного произведения векторов 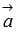и 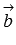равна площади параллелограмма со сторонами и и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.

30. Свойства векторного произведения

Так как векторное произведение в координатах представимо в виде определителя матрицы , то на основании свойств определителя легко обосновываются следующие свойства векторного произведения:

Не нашли, что искали? Воспользуйтесь поиском: