Свойства линейно зависимых и линейно независимых векторов 4 страница

67.Уравнение прямой, проходящей через 2 точки.

69.Нормальное уравнение прямой.

Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.

Если - полярный угол нормали, р - длина отрезка (рис.), то уравнение данной прямой может быть записано в виде

;

уравнение этого вида называется нормальным.

70.Привидение общего уравнения прямой к нормальному виду.

Если дано общее уравнение прямой , то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель , определяемый формулой

.

Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

71.Расстояние от точки до прямой.

Расстояние от точки до прямой. Пусть прямая на плоскости задана уравнением и точка имеет координаты (рис. 25). Обозначим – основание перпендикуляра, опущенного из точки на прямую , , – расстояние от точки до прямой . Тогда , а – нормальный вектор прямой. Рассмотрим скалярное произведение . С одной стороны, , так как , следовательно, угол между ними или . С другой стороны, , но точка , поэтому ее координаты удовлетворяют уравнению , откуда , поэтому . Приравнивая выражения, получим

. Тогда или .

72. Кривые второго порядка.

73. Определение, что такое кривая второго порядка.

Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка

(12.1)

где -- вещественные числа, и хотя бы одно из чисел

отлично от нуля.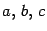

Исследование уравнения (12.1) в общем виде проводится так же, как и для аналогичного уравнения в пространстве (поверхности второго порядка) и эти исследования удобно производить с помощью математического аппарата, который будет рассмотрен позже. Здесь же мы ограничимся констатацией того, что уравнение (12.1) в зависимости от коэффициентов может задавать только четыре типа кривых, а именно, окружность, эллипс, гиперболу и параболу. Изучению этих кривых в "удобной" системе координат и посвящена данная глава.

74. Вывод уравнения эллипса.

Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2 c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a ² - b ² = c ².

75. Исследование формы эллипса по его уравнению.

76. Эксцентриситет. Директрисы. Параметрическое уравнение эллипса.

Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения

или . (13)

рис.8.

Теорема. Пусть М – произвольная точка эллипса, , – ее фокальные радиусы, – расстояние от точки М до левой директрисы, – до правой. Тогда

, (14)

где – эксцентриситет эллипса.

Доказательство.

рис.9.

Пусть М(х, у) – координаты произвольной точки эллипса. Тогда

, ,

откуда и следуют равенства (14).

Каноническое уравнение эллипса может быть параметризовано:

где — параметр уравнения.

В случае окружности параметр является углом между радиус-вектором данной точки и положительным направлением оси абсцисс.

77. Вывод уравнения гиперболы.

78. Исследование формы гиперболы по его уравнению

79. Эксцентриситет. Директрисы. Асимптоты.

Уравнение гиперболы, изображенной на рисунке .

Параметры:
a, b – полуоси;
- расстояние между фокусами,
- эксцентриситет;
- асимптоты;
- директрисы.
Прямоугольник, изображенный в центре рисунка – основной прямоугольник, его диагонали есть асимптоты.

Уравнение гиперболы, изображенной на рисунке .

Параметры:
a, b – полуоси;
- расстояние между фокусами,
- эксцентриситет;
- асимптоты;
- директрисы.
Прямоугольник, изображенный в центре рисунка – основной прямоугольник, его диагонали есть асимптоты.

80. Вывод уравнения параболы.

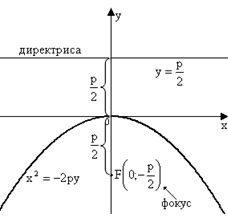
81. Исследование формы параболы по её уравнению.

93. Математический анализ.

94. Действительная функция действительного аргумента. Основные элементарные функции.

1. постоянная ;

2. степенная , задано;

3. показательная ;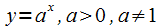

4. логарифмическая ;

5. тригонометрические ;

6. обратные тригонометрические ;

95. Понятие о множестве.

96. Множество на числовой прямой.

97. Интервал, отрезок.

98. Понятие функции действительного переменного

99. Способы задания функции.

100. Основные элементарные функции.

101. Классификация элементарных функций.

102. Числовая последовательность, ее предел. Критерий Вейерштрасса.

ВЕЙЕРШТРАССА КРИТЕРИЙ минимальности поверхности: для того чтобы двумерная поверхность в n-мерном евклидовом пространстве Еⁿ, n ≥ 3, принадлежащая в изотермич. координатах u и v классу С², была минимальной, необходимо и достаточно, чтобы компоненты ее радиус-вектора были гармонич. функциями (u, v).

103. Дискретные функции.

104. Числовая последовательность.

105. Понятие предела числовой последовательности.

106. Свойства сходящихся последовательностей.

107. Критерий Вейерштрасса.

108. Предельный переход в неравенстве и равенстве.

109. Арифметические операции над последовательностями.

110. Число е.

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера.

111. Предел функции. Бесконечно малые и бесконечно большие величины и их свойства.

такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Теорема 1. Алгебраическая сумма конечного числа бесконечно малых при x ® а функций есть функция бесконечно малая при x ® а.

Доказательство. Для простоты ограничимся двумя функциями:

a(x) ® 0, b(x) ® 0 при x ® a.

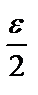Пусть e > 0 – произвольное число. Тогда число тоже произвольное положительное число. Из условий: a(x) ®0, b(x) ®0 при x ® a следует, что для числа существуют б-окрестности точки а O₁ (а, б) и О₂ (а, б) такие, что < для x Î O₁ (а, б), а ï b(x) ï < для x Î O₂ (а, б). В О (а, б) = О₁ (а, б) Ç О₂ (а, б) будут одновременно выполнены оба последних неравенства.

Таким образом, ï a(x) + b(х) ï £ ï a(x) ï + ï b(x) ï < для x Î O (а, б), что и означает, что , то есть a(x) + b(x) – бесконечно малая при x ® a.

Теорема 2. Произведение конечного числа бесконечно малых при x ® a функций есть бесконечно малая при x ® a функция.

Теорема 3. Произведение бесконечно малой при x ® a функции на функцию, ограниченную при x ® a, есть бесконечно малая при x ® a.

Следствие. Целая положительная степень [ a (x)]ⁿ бесконечно малой при x ® a функции a(x) есть бесконечно малая при x ® a.

112. Понятие конечного предела функции.

113. Понятие предела функции при х->inf.

114. Бесконечные пределы.

Определение 1. Функция y=f(x) имеет предел при , равный +¥ (-¥), если "М>0 $ такое, что при всех х, удовлетворяющих , выполняется неравенство f(x)>М (f(x)<-М).

Определение 2. Число А называется пределом функции y=f(x) при слева, или левосторонним пределом, если "e>0 $ такое, что при всех х, удовлетворяющих условно , выполняется неравенство |f(x)-А|<e.

Определение 3. Число А называется пределом функции y=f(x) при справа, или правосторонним пределом, если "e>0 $ такое, что при всех х, удовлетворяющих неравенству , выполняется неравенство |f(x)-А|<e.

115. Ограниченные функции

Ограниченная функция. Пусть функция (одного или многих переменных) определена на множестве D. Если множество ее значений ограничено, когда аргумент (аргументы) пробегают все множество D, функция называется ограниченной. Соответственно, если множество значений функции ограничено сверху (снизу), то функция также называется ограниченной сверху (снизу).

116. Предел монотонной функции.

117. Бесконечно малые и бесконечно большие величины.

Лемма. Если f(х) ¥ при х а, то 0 при х ® а. Если a (x) ® 0 при x ® a, то ® ¥ при x ® a и a (x) ¹ 0.

Действительно, пусть f(x) ® ¥, то есть является бесконечно большой. Тогда ï f(x) ï > М для x Î O (а, б). для x Î O (а, б), то есть для x Î O (а, б), это означает, что , так как можно взять в качестве e > 0.

Аналогично доказывается вторая часть утверждения.

Теорема 1. Алгебраическая сумма конечного числа бесконечно малых при x ® а функций есть функция бесконечно малая при x ® а.

Доказательство. Для простоты ограничимся двумя функциями:

a(x) ® 0, b(x) ® 0 при x ® a.

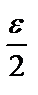Пусть e > 0 – произвольное число. Тогда число тоже произвольное положительное число. Из условий: a(x) ®0, b(x) ®0 при x ® a следует, что для числа существуют б-окрестности точки а O₁ (а, б) и О₂ (а, б) такие, что < для x Î O₁ (а, б), а ï b(x) ï < для x Î O₂ (а, б). В О (а, б) = О₁ (а, б) Ç О₂ (а, б) будут одновременно выполнены оба последних неравенства.

Таким образом, ï a(x) + b(х) ï £ ï a(x) ï + ï b(x) ï < для x Î O (а, б), что и означает, что , то есть a(x) + b(x) – бесконечно малая при x ® a.

Теорема 2. Произведение конечного числа бесконечно малых при x ® a функций есть бесконечно малая при x ® a функция.

Теорема 3. Произведение бесконечно малой при x ® a функции на функцию, ограниченную при x ® a, есть бесконечно малая при x ® a.

Следствие. Целая положительная степень [ a (x)]ⁿ бесконечно малой при x ® a функции a(x) есть бесконечно малая при x ® a.

Две бесконечно малые при х а функции a(х) и b(х) называются бесконечно малыми одинакового порядка, если k, где k ¹0 и конечно.

Например, функции у = х +1 и у = х ^з+1 при х -1 являются бесконечно малыми одинакового порядка, так как .

Две бесконечно малые при х а функции a(х) и b(х) называются эквивалентными при х а, если , то есть a (x)» b(x) при x ® a.

Бесконечно малая при х а функция a(х) называется функцией более высокого порядка по сравнению с функцией b(х) при х а, если .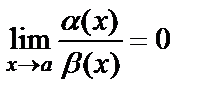

В этом случае пишут a(х) = о (b(х)).

Так, функция y = х ³ является бесконечно малой более высокого порядка по сравнению с y = х при х 0, так как .

Замечание. Если , то в силу определения предела функции получаем: ï f(x)-A ï<e при x Î O(а, б), что означает, что f(x) – A является бесконечно малой при x ® a. Тогда, полагая f(x)-A=a(x), имеем f(x) = A + a(x), где a(x) ® 0 при x ® a.

Таким образом, имеем:

= A <=> f(x) = A + a(x), где a(x) 0 при x ® a.

Лемма. Если , то в некоторой окрестности О(а) точки знак функции f(x) (x Î X) совпадает со знаком числа А.

118. Теоремы о связи функции, ее конечного предела и бесконечно малых.

119. Бесконечно большие величины и их свойства.

120. Свойства бесконечно больших величин.

121. Основные теоремы о пределах.

Теорема 1. Если в точке а существуют пределы функций f(x) и g(x), то в этой точке существует и предел суммы f(x) ± g(x), причём .

Теорема 2. Если в точке а существуют пределы функций f (x) и g (x), то существует и предел произведения f(x)×g(х), причем .

Следствие 1. Постоянный множитель можно выносить за знак предела.

Действительно,

Следствие 2.

Теорема 3. Если в точке а существуют пределы функций f(х) и g (x) и при этом , то существует и предел частного , причем .

Теорема 4. Если функция f (x) имеет предел в точке а, отличный от нуля, то функция также имеет в этой точке предел, причем .

122. Первый замечательный предел.

123. Показательно степенная функция и ее предел.

124. Второй замечательный предел.

125. Сравнение бесконечно малых величин.

126. Свойства эквивалентных бесконечно малых величин.

127. Таблица эквивалентных бесконечно малых величин.

128. Непрерывность функции в точке и на множестве.

129. Односторонние пределы.

130. Точки разрыва функции и их классификация.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел и правосторонний предел ;
• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу:

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

131. Основные теоремы о непрерывных функциях.

132. Непрерывность и разрывы монотонной функции.

133. Свойства функций непрерывных на отрезке.

134. Понятие производной.

135. Общее правило нахождения производной.

136. Механический смысл производной.

137. Геометрический смысл производной.

138. Уравнение касательной и нормали к кривой.

139. Связь между непрерывность. И дифференцированием функции.

140. Основные правила дифференцирования. Теоремы.

141. Производные основных элементарных функций.

142. Дифференцирование неявных функций.

143. Логарифмическое дифференцирование.

144. Дифференцирование параметрических функций.

145. Производные высших порядков.

146. Понятие дифференциала функции.

147. Геометрический смысл дифференциала.

148. Дифференциалы основных элементарных функций и их правила вычисления.

149. Применение дифференциала к приближенному вычислению.

150. Дифференциал сложной функции. Инвариантность формы первого дифференциала.

151. Дифференциалы высших порядков.

152. Основные теоремы дифференциального исчисления. Теорема Ферма. Теорема Ролля. Теорема Коши. Теорема Лагранжа.

Не нашли, что искали? Воспользуйтесь поиском: