
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства линейно зависимых и линейно независимых векторов 2 страница
1. антикоммутативность 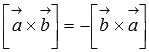 ;
;
2. свойство дистрибутивности  или
или  ;
;
3. сочетательное свойство 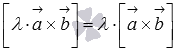 или
или 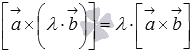 , где
, где  - произвольное действительное число.
- произвольное действительное число.
Для примера докажем свойство антикоммутативности векторного произведения.
По определению  и
и  . Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому,
. Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому,  , что доказывает свойство антикоммутативности векторного произведения.
, что доказывает свойство антикоммутативности векторного произведения.
31. Теорема о необходимом и достаточном условии коллинеарности 2 векторов.
для коллинеарности двух векторов a и b необходимо и достаточно, чтобы они были связаны равенствами  или
или  .
.
Перейдем к координатной форме полученного условия коллинеарности двух векторов.
Пусть вектор a задан в прямоугольной декартовой системе координат на плоскости и имеет координаты  , тогда вектор
, тогда вектор  имеет координаты
имеет координаты  (при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор a задан в прямоугольной системе координат трехмерного пространства как
(при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор a задан в прямоугольной системе координат трехмерного пространства как  , то вектор
, то вектор  имеет координаты
имеет координаты  .
.
Следовательно, для коллинеарности двух ненулевых векторов  и
и  на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:
на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: 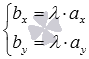 или
или  .
.
Для коллинеарности двух ненулевых векторов  и
и  в пространстве необходимо и достаточно, чтобы
в пространстве необходимо и достаточно, чтобы  или
или  .
.
Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов  и
и  .
.
Если ненулевые векторы  и
и  коллинеарны, то по определению векторного произведения
коллинеарны, то по определению векторного произведения 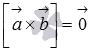 , что равносильно равенству
, что равносильно равенству  . А последнее равенство возможно лишь тогда, когда векторы
. А последнее равенство возможно лишь тогда, когда векторы  и
и  связаны соотношениями
связаны соотношениями  или
или  , где
, где 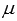 - произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов a и b. Таким образом, два ненулевых вектора a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
- произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов a и b. Таким образом, два ненулевых вектора a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
32. Выражение векторного произведения через координаты сомножителей.
В основном встречаются три типа задач.
В задачах первого типа заданы длины двух векторов и угол между ними, а требуется найти длину векторного произведения. В этом случае используется формула  .
.
Задачи второго типа связаны с координатами векторов, в них векторное произведение, его длина или что-либо еще ищется через координаты заданных векторов 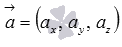 и
и  .
.
Здесь возможна масса различных вариантов. К примеру, могут быть заданы не координаты векторов 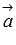 и
и 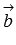 , а их разложения по координатным векторам вида
, а их разложения по координатным векторам вида  и
и  , или векторы a и b могут быть заданы координатами точек их начала и конца.
, или векторы a и b могут быть заданы координатами точек их начала и конца.
33. Физический смысл векторного произведения
Моментом силы  , приложенной к точке B, относительно точки А называется векторное произведение
, приложенной к точке B, относительно точки А называется векторное произведение  .
.
34. Смешанное произведение векторов.
35. Основные понятия
Смешанным, или векторно-скалярным произведением трех векторов (обозначается  ) называется произведение вида
) называется произведение вида  .
.
36. Геометрический смысл
Выясним геометрический смысл смешанного произведения векторов 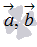 и
и  .
.
Отложим векторы 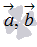 и
и  от одной точки и построим параллелепипед на этих векторах как на сторонах.
от одной точки и построим параллелепипед на этих векторах как на сторонах.
Обозначим 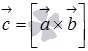 . В этом случае смешанное произведение можно записать как
. В этом случае смешанное произведение можно записать как  , где
, где  - числовая проекция вектора
- числовая проекция вектора  на направление вектора
на направление вектора 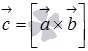 .
.
Абсолютная величина числовой проекции  равна высоте параллелепипеда, построенного на векторах
равна высоте параллелепипеда, построенного на векторах 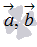 и
и  , так как вектор
, так как вектор 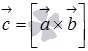 перпендикулярен и вектору
перпендикулярен и вектору 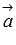 и вектору
и вектору 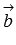 по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина
по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина  представляет собой площадь параллелограмма, построенного на векторах
представляет собой площадь параллелограмма, построенного на векторах 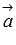 и
и 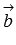 . Таким образом, модуль смешанного произведения
. Таким образом, модуль смешанного произведения  - это произведение площади основания на высоту параллелепипеда, построенного на векторах
- это произведение площади основания на высоту параллелепипеда, построенного на векторах 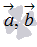 и
и  .
.
Следовательно, абсолютная величина смешанного произведения векторов представляет собой объем параллелепипеда:  . В этом заключается геометрический смысл смешанного произведения векторов.
. В этом заключается геометрический смысл смешанного произведения векторов.
Объем тетраэдра, построенного на векторах 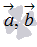 и
и  , равен одной шестой объема соответствующего параллелепипеда, таким образом,
, равен одной шестой объема соответствующего параллелепипеда, таким образом,  .
.

37. Выражение смешанного произведения через координаты сомножителей.
Смешанным, или векторно-скалярным произведением трех векторов (обозначается  ) называется произведение вида
) называется произведение вида  .
.
Пусть известны координаты векторов:  ,
,  ,
,  . Векторное произведение векторов
. Векторное произведение векторов  и
и 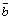 – это вектор с координатами
– это вектор с координатами 
 .
.
Скалярное произведение вектора  на вектор
на вектор  :
: 
Таким образом,
 . (2.11)
. (2.11)
Нетрудно показать, что  .
.
Отложим данные некомпланарные векторы  ,
,  ,
, 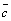 от общего начала и построим на них как на ребрах параллелепипед (рис. 18).
от общего начала и построим на них как на ребрах параллелепипед (рис. 18).

Рис. 18
По определению скалярного произведения 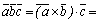
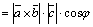 , где
, где  – угол между векторами
– угол между векторами  и
и  . Но
. Но  – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах  и
и  , а
, а 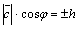 , где
, где  – высота параллелепипеда. Таким образом,
– высота параллелепипеда. Таким образом,  .
.
Смешанное произведение трех векторов с точностью до знака равно объему параллелепипеда, построенного на этих векторах как на ребрах. Можно записать: 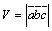 .
.
Объем тетраэдра, построенного на векторах  ,
,  ,
, 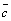 (рис. 19) равен
(рис. 19) равен  .
.
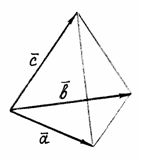
Рис. 19
Заметим, что если векторы  ,
,  ,
, 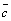 образуют правую тройку, то
образуют правую тройку, то  и
и  , а если левую, то
, а если левую, то  и
и 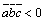 .
.
38. Свойства смешанного произведения
Из свойств векторного произведения и свойств скалярного произведения следуют следующие свойства смешанного произведения:
1.
 ;
;
2.
 ;
;
3.

Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.
Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.
Действительно, если  , то по определению векторного произведения
, то по определению векторного произведения  , следовательно, смешанное произведение равно нулю, так как
, следовательно, смешанное произведение равно нулю, так как  . Если же
. Если же  или
или  , то угол между векторами
, то угол между векторами  и
и  равен
равен  , следовательно, по определению скалярного произведения векторов
, следовательно, по определению скалярного произведения векторов  .
.
Свойства смешанного произведения обычно применяются при доказательстве тождеств или неравенств.
39. Теорема о необходимом и достаточном условии компланарности двух векторов.
Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Доказательство. Необходимость. Пусть векторы  ,
,  ,
, 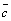 компланарны. Можно считать, что они лежат в одной плоскости. Тогда вектор
компланарны. Можно считать, что они лежат в одной плоскости. Тогда вектор 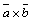 перпендикулярен этой плоскости, следовательно,
перпендикулярен этой плоскости, следовательно, 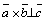 ,
,
а значит, их скалярное произведение равно нулю, то есть  .
.
Достаточность. Пусть  . Предположим, что векторы некомпланарны. Но тогда существует параллелепипед, построенный на этих векторах, объем которого
. Предположим, что векторы некомпланарны. Но тогда существует параллелепипед, построенный на этих векторах, объем которого  , а это противоречит условию
, а это противоречит условию  . Следовательно, предположение неверно, и векторы компланарны.
. Следовательно, предположение неверно, и векторы компланарны.
40. Аналитическая геометрия
41. Полярная система координат
Полярная система координат на плоскости определяется заданием некоторой точки О, называемой полюсом, луча Ор, исходящего из этой точки и называемого полярной осью, и единицы масштаба  (рис. 39).
(рис. 39).
Пусть М – произвольная точка плоскости. Обозначим = ОМ – расстояние точки М от полюса,  – угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ. Числа и называются полярными координатами точки М, – полярный радиус, – полярный угол точки М. По определению 0. Задание пары чисел (, ) однозначно определяет точку М на плоскости. Если ограничить изменение пределами 0 2 (или - ), то каждой точке плоскости также будет однозначно соответствовать пара чисел (, ). Исключение составляет полюс, для которого = 0, а угол не определен.
– угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ. Числа и называются полярными координатами точки М, – полярный радиус, – полярный угол точки М. По определению 0. Задание пары чисел (, ) однозначно определяет точку М на плоскости. Если ограничить изменение пределами 0 2 (или - ), то каждой точке плоскости также будет однозначно соответствовать пара чисел (, ). Исключение составляет полюс, для которого = 0, а угол не определен.

Рис. 39
42. Связь между полярными и декартовыми координатами
Выберем декартову систему координат так, чтобы ее начало 0 совпадало с полюсом, а ось ОХ была направлена по полярной оси Ор (рис.40). Тогда полярные координаты (, ) и декартовы координаты (х, у) точки М связаны соотношениями:

| (2.25) |

| (2.26) |
Из этих формул следует:

| (2.27) |
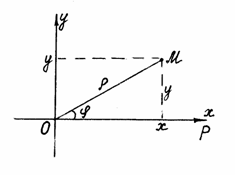
Рис. 40
Формула для tg определяет два угла и + в промежутке [0; 2). Чтобы уточнить, какой из углов выбрать, нужно учесть четверть, в которой находится точка М, или воспользоваться формулами (2.27).
Чтобы перейти от уравнения линии в декартовых координатах к ее полярному уравнению, нужно вместо х, у подставить в уравнение их выражения из формул (2.25). Обратный переход от полярного уравнения к уравнению в декартовых координатах осуществляется с помощью формул (2.26), (2.27).
43. Уравнение плоскости, проходящей через заданную точку.
Пусть Мо(хо, уо, zо) – заданная точка в плоскости ,  = (А; В; С) – вектор, перпендикулярный плоскости , его называют нормальным вектором плоскости, и пусть М(х, у, z) – произвольная точка плоскости (рис. 43). Тогда
= (А; В; С) – вектор, перпендикулярный плоскости , его называют нормальным вектором плоскости, и пусть М(х, у, z) – произвольная точка плоскости (рис. 43). Тогда 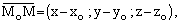
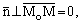 то есть
то есть

| (2.28) |
(2.28) – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

44. Общее уравнение плоскости. Доказательство теорем.

| |
Всякое уравнение вида  , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением вида
, где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением вида  при некотором наборе чисел A, B, C и D.
при некотором наборе чисел A, B, C и D.
ДОКАЗАТЕЛЬСТВО!
Как видите, теорема состоит из двух частей. В первой части нам дано уравнение  и нужно доказать, что оно определяет плоскость. Во второй части, нам дана некоторая плоскость и требуется доказать, что ее можно определить уравнением
и нужно доказать, что оно определяет плоскость. Во второй части, нам дана некоторая плоскость и требуется доказать, что ее можно определить уравнением  при некотором выборе чисел А, В, С и D.
при некотором выборе чисел А, В, С и D.
Начнем с доказательства первой части теоремы.
Так как числа А, В и С одновременно не равны нулю, то существует точка  , координаты которой удовлетворяют уравнению
, координаты которой удовлетворяют уравнению  , то есть, справедливо равенство
, то есть, справедливо равенство  . Отнимем левую и правую части полученного равенства соответственно от левой и правой частей уравнения
. Отнимем левую и правую части полученного равенства соответственно от левой и правой частей уравнения  , при этом получим уравнение вида
, при этом получим уравнение вида  эквивалентное исходному уравнению
эквивалентное исходному уравнению  . Теперь, если мы докажем, что уравнение
. Теперь, если мы докажем, что уравнение  определяет плоскость, то этим будет доказано, что эквивалентное ему уравнение
определяет плоскость, то этим будет доказано, что эквивалентное ему уравнение  также определяет плоскость в заданной прямоугольной системе координат в трехмерном пространстве.
также определяет плоскость в заданной прямоугольной системе координат в трехмерном пространстве.
Равенство  представляет собой необходимое и достаточное условие перпендикулярности векторов
представляет собой необходимое и достаточное условие перпендикулярности векторов 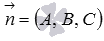 и
и  . Иными словами, координаты плавающей точки
. Иными словами, координаты плавающей точки  удовлетворяют уравнению
удовлетворяют уравнению  тогда и только тогда, когда перпендикулярны векторы
тогда и только тогда, когда перпендикулярны векторы 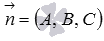 и
и  . Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство
. Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство  , то множество точек
, то множество точек  определяет плоскость, нормальным вектором которой является
определяет плоскость, нормальным вектором которой является 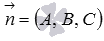 , причем эта плоскость проходит через точку
, причем эта плоскость проходит через точку  . Другими словами, уравнение
. Другими словами, уравнение  определяет в прямоугольной системе координатOxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнение
определяет в прямоугольной системе координатOxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнение  определяет эту же плоскость. Первая часть теоремы доказана.
определяет эту же плоскость. Первая часть теоремы доказана.

Приступим к доказательству второй части.
Пусть нам дана плоскость, проходящая через точку  , нормальным вектором которой является
, нормальным вектором которой является 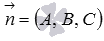 . Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида
. Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида  .
.
Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет  . Тогда векторы
. Тогда векторы 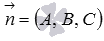 и
и  будут перпендикулярны, следовательно, их скалярное произведение будет равно нулю:
будут перпендикулярны, следовательно, их скалярное произведение будет равно нулю:  . Приняв
. Приняв  , уравнение примет вид
, уравнение примет вид  . Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.
. Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.
45. Частный случай общего уравнения плоскости.
Частные случаи общего уравнения плоскости:
1) By + Cz + D = 0 - параллельна оси Ox;
2) Ax + Cz + D = 0 - параллельна оси Oy;
3) Ax + By + D = 0 - параллельна оси Oz;
4) Cz + D = 0 - параллельна оси Oxy;
5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz;
7) Ax + By + Cz = 0 - проходит через начало координат; Найти сумму ряда.
8) By + Cz = 0 - проходит через ось Ox;
9) Ax + Cz = 0 - проходит через ось Oy;
10) Ax + By = 0 - проходит через ось Oz;
11) z = 0 - плоскость Oxy;
12) y = 0 - плоскость Oxz;
13) x = 0 - плоскость Oyz.
46. Взаимное расположение плоскостей. Угол между двумя плоскостями.
Пусть плоскости 1 и 2 заданы соответственно уравнениями 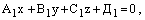
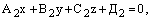 где
где 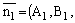
 и
и  – нормальные векторы этих плоскостей (рис. 45). Очевидно,
– нормальные векторы этих плоскостей (рис. 45). Очевидно,  тогда косинус угла между плоскостями
тогда косинус угла между плоскостями
Не нашли, что искали? Воспользуйтесь поиском: