
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства линейно зависимых и линейно независимых векторов 5 страница
153. Правило Лопиталя. Раскрытие неопределенностей 0/0, inf/inf. Другие виды неопределенностей.
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа 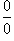 или
или 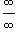 .
.
Пусть a является некоторым конечным действительным числом или равно бесконечности.
Если 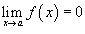 и
и 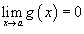 , то
, то 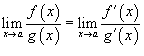 ;
;
Если 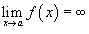 и
и 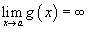 , то аналогично
, то аналогично 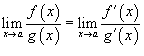 .
.
| Это правило впервые упоминалось в книге по дифференциальному исчислению, опубликованной в 1696 (!) году французским математиком Гийомом Лопиталем (1661- 1704). |
Правило Лопиталя можно также применять к неопределенностям типа 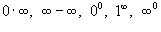 . Первые две неопределенности
. Первые две неопределенности 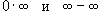 можно свести к типу
можно свести к типу 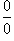 или
или 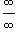 с помощью алгебраических преобразований. А неопределенности
с помощью алгебраических преобразований. А неопределенности 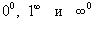 сводятся к типу
сводятся к типу 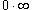 с помощью соотношения
с помощью соотношения
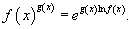
Правило Лопиталя справедливо также и для односторонних пределов.
154. Необходимое и достаточное условие постоянства функции.
Теорема
Пусть функция f (x) определена в промежутке X и имеет внутри него конечную производную f /(x), а на концах (если они принадлежат X) сохраняет непрерывность. Для того чтобы f (x) была в X постоянной, достаточно условие f /(x)=0 внутри X.
Доказательство
Пусть это условие выполнено. Фиксируем некоторую точку x 0 из промежутка X и возьмем любую другую его точку x. Для промежутка [х0,х] или [х,х0] удовлетворены все условия теоремы Лагранжа. Следовательно, можем написать
f (x)− f (x 0)= f /(c)(x − x 0),
где c содержится между x 0 и x, а значит, заведомо лежит внутри X. Но, по предположению, f /(c)=0, так что для всех x из X
f (x)= f (x 0)= const.
Теорема доказана.
Заметим, что высказанное условие, очевидно, является и необходимым для постоянства функции.
Следствие. Пусть две функции f (x) и g (x) определены в промежутке X и внутри него имеют конечные производные f /(x) и g /(x), а на концах (если они принадлежат X) сохраняют непрерывность. Если при этом f /(x)= g /(x) внутри X,
то во всем промежутке X эти функции разнятся лишь на постоянную:
f (x)= g (x)+ C (С = const).
Для доказательства достаточно применить теорему к разности f (x)− g (x), так как ее производная f /(x)− g /(x) внутри X сводится к нулю, то сама разность в X будет постоянной.
155. Монотонность функции на интервале
156. Необходимое и достаточное условие монотонности функции.
Теорема (достаточное условие)
Если функция f(x) дифференцируема на (a,b) и f/(x)≥0 (f/(x)≤0) на (a,b), то f(x) не убывает (не возрастает) на (a,b).
Доказательство
Рассмотрим случай когда f/(x)≥0. Рассмотрим две точки x1,x2∈(a,b) и применим формулу Лагранжа. На [x1,x2] функция f(x) удовлетворяет всем условиям этой теоремы. Следует, чтоx1<x2:
f(x2)−f(x1)=f/(c)(x2−x1), где c∈(x1,x2) и правая часть больше нуля, значит f(x2)−f(x1)≥0 или f(x2)≥f(x1) при x2>x1, функция не убывает.
Теорема доказана.
Замечание
Если требовать, что f/(x)>0 (f/(x)<0), тогда функция строго возрастает (убывает).
157. Экстремумы функции. Основные определения.
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) > 0
(f ' (x) < 0).
Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
158. Необходимое условие существования экстремумов функции.
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
159. Первое достаточное условие существования экстремумов.
Первое достаточное условие. Пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
160. Второе достаточное условие существования экстремумов.
Второе достаточное условие. Пусть функция f(x) имеет производную
f ' (x) в окрестности точки xо и вторую производную 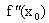 в самой точке xо. Если f ' (xо) = 0,
в самой точке xо. Если f ' (xо) = 0, 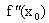 >0 (
>0 ( 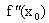 <0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же
<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же 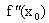 =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
161. Наибольшее и наименьшее значение функции на отрезке.
Наибольшим значением функции y = f(x) на промежутке X называют такое значение 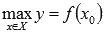 , что для любого
, что для любого 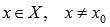 справедливо неравенство
справедливо неравенство 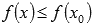 .
.
Наименьшим значением функции y = f(x) на промежутке X называют такое значение 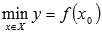 , что для любого
, что для любого 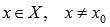 справедливо неравенство
справедливо неравенство 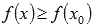 .
.
162. Направление выпуклости и вогнутости кривой. Основные определения.
163. Достаточное условие выпуклости и вогнутости кривой.
Пусть функция f (x) дважды дифференцируема (имеет вторую производную) на интервале (a, b), тогда:
если f '' (x) > 0 для любого x 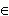 (a, b), то функция f (x) является вогнутой на интервале (a, b);
(a, b), то функция f (x) является вогнутой на интервале (a, b);
если f '' (x) < 0 для любого x 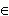 (a, b), то функция f (x) является выпуклой на интервале (a, b).
(a, b), то функция f (x) является выпуклой на интервале (a, b).
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x 0 существует вторая производная f '' (x 0), то f '' (x 0) = 0.
| Рассмотрим график функции y = x 3 : Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6 x, но 6 x > 0 при x > 0 и 6 x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x 3 является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x 3. |
164. Точки перегиба графика функции. Достаточное условие точек перегиба.
Точка перегиба функции 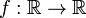 внутренняя точка
внутренняя точка  области определения
области определения 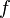 , такая что
, такая что 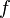 непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и
непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и  является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки  , имеет в
, имеет в  точку перегиба, то
точку перегиба, то 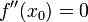 .
.
Достаточное условие существования точки перегиба: если функция 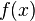 в некоторой окрестности точки
в некоторой окрестности точки 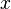
 раз непрерывно дифференцируема, причем
раз непрерывно дифференцируема, причем  нечётно и
нечётно и 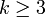 , и
, и 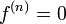 при
при 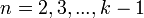 , а
, а 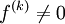 , то функция
, то функция 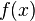 имеет в
имеет в  точку перегиба.
точку перегиба.
165. Асимптоты кривой. Вертикальные асимптоты. Наклонные асимптоты.
Аси́мпто́та кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед[3].
Вертикальная
Вертикальная асимптота — прямая вида 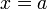 при условии существования предела
при условии существования предела 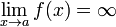 .
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
1. 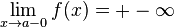
2. 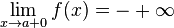
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.
Горизонтальная
Горизонтальная асимптота — прямая вида 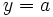 при условии существования предела
при условии существования предела
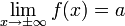 .
.
Наклонная
Наклонная асимптота — прямая вида 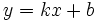 при условии существования пределов
при условии существования пределов
Пример наклонной асимптоты
1. 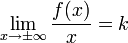
2. 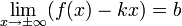
Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!
Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен 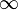 ), то наклонной асимптоты при
), то наклонной асимптоты при 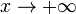 (или
(или 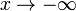 ) не существует!
) не существует!
166. Формула Тейлора для многочлена.

167. Формула Тейлора для произвольной функции.
168. Остаточный член формулы Тейлора в формуле Лагранжа.
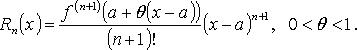
169. Формулы Тейлора и Маклорена. Представление по формулам Маклорена основных элементарных функций.
Формула Тейлора и Маклорена. 
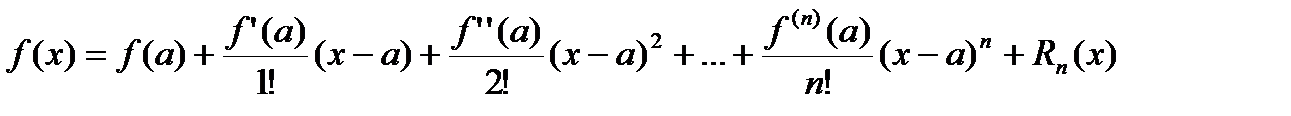
Формула Тейлора
f(x)= P(x) - 
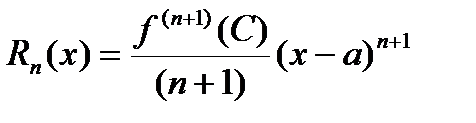
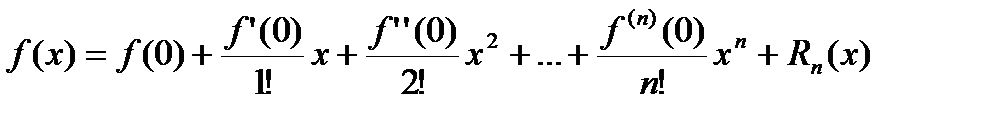
Формула Маклорена
Не нашли, что искали? Воспользуйтесь поиском: