
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства линейно зависимых и линейно независимых векторов 3 страница
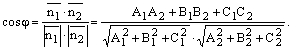
| (2.32) |

Рис. 45
Если 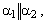 то
то  – условие параллельности плоскостей.
– условие параллельности плоскостей.
Если  то
то  то есть
то есть  – условие перпендикулярности плоскостей.
– условие перпендикулярности плоскостей.
47. Уравнение плоскости проходящей через три точки
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, в ней заданы три несовпадающие точки  , которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.
, которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.
Покажем два способа ее решения.
Первый способ составления уравнения плоскости, проходящей через три заданные точки  .
.
Известно, что общее уравнение плоскости вида  задает в прямоугольной системе координат Oxyz плоскость
задает в прямоугольной системе координат Oxyz плоскость  , которая проходит через точку
, которая проходит через точку  , а нормальный вектор плоскости
, а нормальный вектор плоскости  имеет координаты
имеет координаты  . Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки
. Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки  .
.
Итак, из условия задачи нам известны координаты точки (даже координаты трех точек), через которую проходит плоскость, уравнение которой нам требуется составить. Осталось отыскать координаты нормального вектора  этой плоскости.
этой плоскости.
Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости перпендикулярны, то вектор  перпендикулярен как вектору
перпендикулярен как вектору  , так и вектору
, так и вектору  . Следовательно, в качестве вектора
. Следовательно, в качестве вектора  можно принять векторное произведение векторов
можно принять векторное произведение векторов  и
и  . Так как
. Так как  и
и  (при необходимости обращайтесь к статье вычисление координат вектора по координатам точек), то
(при необходимости обращайтесь к статье вычисление координат вектора по координатам точек), то  . После вычисления записанного определителя, станут видны координаты нормального вектора
. После вычисления записанного определителя, станут видны координаты нормального вектора  , и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.
, и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.
48. Уравнение плоскости в отрезках.
 , где a, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках. Такое название не случайно. Абсолютные величины чисел a, b и c равны длинам отрезков, которые плоскость отсекает на координатных осях Ox, Oy и Oz соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) откладываются отрезки на координатных осях. Действительно, координаты точек
, где a, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках. Такое название не случайно. Абсолютные величины чисел a, b и c равны длинам отрезков, которые плоскость отсекает на координатных осях Ox, Oy и Oz соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) откладываются отрезки на координатных осях. Действительно, координаты точек 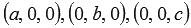 удовлетворяют уравнению плоскости в отрезках:
удовлетворяют уравнению плоскости в отрезках:

Посмотрите на рисунок, поясняющий этот момент.
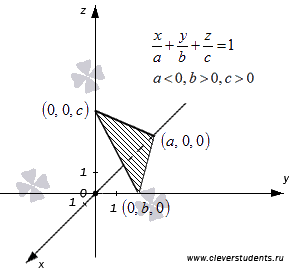
49. Нормальное уравнение плоскости
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz.
Рассмотрим плоскость, которая удалена на расстояние p (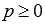 ) единиц от начала координат в положительном направлении нормального вектора плоскости
) единиц от начала координат в положительном направлении нормального вектора плоскости  . Будем считать, что длина вектора
. Будем считать, что длина вектора  равна единице. Тогда его координаты равны направляющим косинусам, то есть,
равна единице. Тогда его координаты равны направляющим косинусам, то есть, 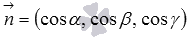 , причем
, причем  . Обозначим расстояние от точки до плоскости как
. Обозначим расстояние от точки до плоскости как  , то есть, точка N лежит на плоскости и длина отрезка ON равна p. Для наглядности отметим все данные на чертеже.
, то есть, точка N лежит на плоскости и длина отрезка ON равна p. Для наглядности отметим все данные на чертеже.
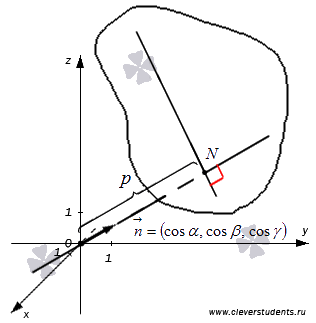
Получим уравнение этой плоскости.
Возьмем точку трехмерного пространства  . Тогда ее радиус вектор
. Тогда ее радиус вектор  имеет координаты
имеет координаты  , то есть,
, то есть,  (при необходимости смотрите разделкоординаты радиус-вектора точки). Очевидно, что множество точек
(при необходимости смотрите разделкоординаты радиус-вектора точки). Очевидно, что множество точек  определяют описанную ранее плоскость тогда и только тогда, когда числовая проекция вектора
определяют описанную ранее плоскость тогда и только тогда, когда числовая проекция вектора  на направление вектора
на направление вектора  равна p, то есть,
равна p, то есть,  (смотрите рисунок ниже).
(смотрите рисунок ниже).
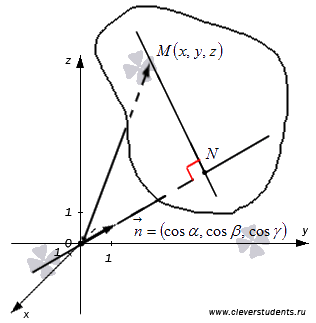
Тогда определение скалярного произведения векторов 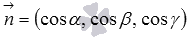 и
и  дает нам следующее равенство
дает нам следующее равенство  . Это же скалярное произведение в координатной форме представляется как
. Это же скалярное произведение в координатной форме представляется как  . Сопоставление двух последних равенств дает нам искомое уравнение плоскости
. Сопоставление двух последних равенств дает нам искомое уравнение плоскости  . Перенесем p в левую часть, и мы получим уравнение
. Перенесем p в левую часть, и мы получим уравнение  , которое называется нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.
, которое называется нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.
Итак, нормальное уравнение плоскости вида  задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости
задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости 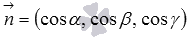 .
.
50. Привидение общего уравнения плоскости к нормальному виду.
Общее уравнение плоскости  может быть приведено к нормальному виду умножением его обеих частей на так называемый нормирующий множитель
может быть приведено к нормальному виду умножением его обеих частей на так называемый нормирующий множитель 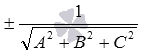 . Знак нормирующего множителя берется противоположным знаку числа D. Если D = 0, то знак нормирующего множителя значения не имеет.
. Знак нормирующего множителя берется противоположным знаку числа D. Если D = 0, то знак нормирующего множителя значения не имеет.
Общее уравнение плоскости после умножения на нормирующий множитель будет действительно нормальным уравнением плоскости, так как длина вектора с координатами  равна единице
равна единице
 ,
,
а правило выбора знака нормирующего множителя гарантирует выполнение условия 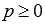 .
.
51. Расстояние от точки до плоскости
Расстояние от точки до плоскости – это расстояние от данной точки до основания перпендикуляра, проведенного из заданной точки к заданной плоскости.
Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.
алгоритм для нахождения расстояния от точки  до плоскости
до плоскости  следующий:
следующий:
· составляем уравнение прямой a, которая проходит через точку М1 и перпендикулярна к плоскости  ;
;
· находим координаты  точки H1 - точки пересечения прямой a и плоскости
точки H1 - точки пересечения прямой a и плоскости  ;
;
· вычисляем расстояние от точки М1 до плоскости  по формуле
по формуле  .
.
52.Уравнение линии в пространстве. Параметрические уравнение линии.
прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей 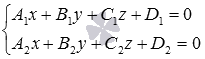
Параметрические уравнения прямой в пространстве имеют вид  , где x1, y1 и z1 – координаты некоторой точки прямой, ax, ay и az (ax, ay и az одновременно не равны нулю) - соответствующие координаты направляющего вектора прямой, а
, где x1, y1 и z1 – координаты некоторой точки прямой, ax, ay и az (ax, ay и az одновременно не равны нулю) - соответствующие координаты направляющего вектора прямой, а  - некоторый параметр, который может принимать любые действительные значения.
- некоторый параметр, который может принимать любые действительные значения.
При любом значении параметра  по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел
по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел  , она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой). К примеру, при
, она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой). К примеру, при  из параметрических уравнений прямой в пространстве получаем Всякое уравнение первой степени вида
из параметрических уравнений прямой в пространстве получаем Всякое уравнение первой степени вида 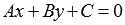 , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида
, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида 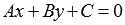 при некотором наборе значений A, B и C. координаты x1, y1 и z1:
при некотором наборе значений A, B и C. координаты x1, y1 и z1:  .
.
53. Общее уравнение прямой линии в пространстве.
Всякое уравнение первой степени вида 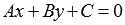 , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида
, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида 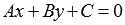 при некотором наборе значений A, B и C.
при некотором наборе значений A, B и C.
54. Векторное уравнение прямой в пространстве
Можно задать прямую в пространстве и другим способом.
Ненулевой вектор, лежащий на прямой (параллельный ей) называется направляющим вектором прямой.
Пусть для прямой 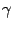 известны ее направляющий вектор
известны ее направляющий вектор  и точка
и точка  , лежащая на этой прямой. Пусть
, лежащая на этой прямой. Пусть  -- произвольная (текущая) точка прямой
-- произвольная (текущая) точка прямой 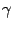 . Обозначим через
. Обозначим через  и r радиус-векторы точек
и r радиус-векторы точек  и
и  соответственно (рис. 11.11).
соответственно (рис. 11.11).

Рис.11.11.Векторное уравнение прямой
Тогда вектор  коллинеарен вектору p и, следовательно,
коллинеарен вектору p и, следовательно,  , где
, где  -- некоторое число. Из рис. 11.11 видно, что
-- некоторое число. Из рис. 11.11 видно, что
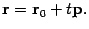
| (11.12) |
Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра  мы будем получать новую точку
мы будем получать новую точку  на прямой
на прямой 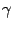
55. Параметрическое уравнение прямой
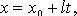
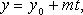
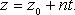
56. Каноническое уравнение прямой в пространстве
Канонические уравнения прямой
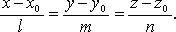
57.Уравнение прямой проходящей через две точки
направляющим вектором прямой a, которая проходит через точки М1 и М2, является вектор  , он имеет координаты
, он имеет координаты 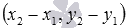 (при необходимости смотрите статьювычисление координат вектора по координатам точек его конца и начала). Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора
(при необходимости смотрите статьювычисление координат вектора по координатам точек его конца и начала). Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора  и координаты лежащей на ней точки
и координаты лежащей на ней точки  (и
(и 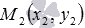 ). Оно имеет вид
). Оно имеет вид 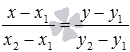 (или
(или  ).
).

Также мы можем записать параметрические уравнения прямой на плоскости, проходящей через две точки  и
и 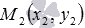 . Они имеют вид
. Они имеют вид 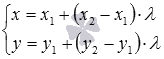 или
или  .
.
58. Угол между двумя прямыми условие параллельности и перпендикулярности прямых.
Пусть прямые  и и  заданы каноническими уравнениями заданы каноническими уравнениями  и и  Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых: Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых: 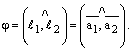 Тогда Тогда
Если Если | ||
59. Приведение общего уравнения прямой к каноническому виду.
Если  , то переносим слагаемое
, то переносим слагаемое  в правую часть равенства
в правую часть равенства 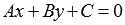 с противоположным знаком
с противоположным знаком  . В левой части равенства выносим А за скобки
. В левой части равенства выносим А за скобки  . Полученное равенство можно записать как пропорцию вида
. Полученное равенство можно записать как пропорцию вида  .
.
Если  , то оставляем в левой части общего уравнения прямой
, то оставляем в левой части общего уравнения прямой 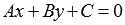 только слагаемое
только слагаемое  , а остальные переносим в правую часть с противоположным знаком:
, а остальные переносим в правую часть с противоположным знаком:  . Теперь выносим в правой части равенства –B за скобки
. Теперь выносим в правой части равенства –B за скобки  и записываем полученное равенство в виде пропорции
и записываем полученное равенство в виде пропорции  . Вот и все.
. Вот и все.
60. Условие параллельности и перпендикулярности прямой и плоскости.
Пусть плоскость задана уравнением 
 – ее нормальный вектор, а прямая
– ее нормальный вектор, а прямая  задана уравнениями
задана уравнениями 
 – направляющий вектор прямой. Обозначим
– направляющий вектор прямой. Обозначим 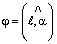 – угол между прямой и плоскостью,
– угол между прямой и плоскостью,  – угол между соответствующими векторами.Очевидно,
– угол между соответствующими векторами.Очевидно, 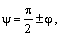 а
а 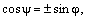 или
или  Но
Но  тогда синус угла между прямой и плоскостью можно найти по формуле
тогда синус угла между прямой и плоскостью можно найти по формуле

| (2.39) |
Если  то
то  (рис. 47), то есть
(рис. 47), то есть  или
или

| (2.40) |
– условие параллельности прямой и плоскости. При этом же условии прямая лежит в плоскости.
Если  то
то  , то есть
, то есть 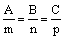 – условие перпендикулярности прямой и плоскости.
– условие перпендикулярности прямой и плоскости.
Пусть требуется найти точку пересечения прямой  и плоскости
и плоскости  Запишем параметрические уравнения прямой
Запишем параметрические уравнения прямой 

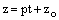 и подставим выражения для х, у, z в уравнение плоскости. Получим уравнение вида
и подставим выражения для х, у, z в уравнение плоскости. Получим уравнение вида  относительно параметра t. Выразив t и подставив в параметрические уравнения, найдем координаты точки пересечения.
относительно параметра t. Выразив t и подставив в параметрические уравнения, найдем координаты точки пересечения.
Замечание. Если уравнение относительно t примет вид 0t = 0 (то есть M = N = 0), то любое действительное значение t будет его решением, значит, прямая и плоскость имеют множество общих точек, то есть прямая лежит в плоскости.
Если уравнение относительно t примет вид 0 t = N (то есть М = 0, N 0), то такое уравнение решений не имеет, значит, прямая и плоскость не имеют общих точек, то есть прямая параллельна плоскости.
61. Общее уравнение прямой.
62. Частные случаи общего уравнения прямой.
Общее уравнение прямой 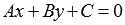 называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным.
называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным.
Рассмотрим все возможные варианты неполного общего уравнения прямой.
При  общее уравнение прямой
общее уравнение прямой 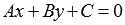 примет вид By+C=0. Это неполное общее уравнение прямой определяет в прямоугольной системе координат Oxy прямую параллельную оси Ох, так как при любых действительных значениях переменной х переменная y принимает одно и то же значение
примет вид By+C=0. Это неполное общее уравнение прямой определяет в прямоугольной системе координат Oxy прямую параллельную оси Ох, так как при любых действительных значениях переменной х переменная y принимает одно и то же значение  . Другими словами, общее уравнение прямой
. Другими словами, общее уравнение прямой 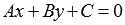 при
при  определяет геометрическое место точек
определяет геометрическое место точек  , ординаты которых равны одному и тому же числу
, ординаты которых равны одному и тому же числу  .
.
При  общее уравнение прямой примет вид y=0. Это общее неполное уравнение прямой определяет ось абсцисс Ox.
общее уравнение прямой примет вид y=0. Это общее неполное уравнение прямой определяет ось абсцисс Ox.
Аналогично, при  имеем неполное общее уравнение прямой вида Ax+C=0. Это уравнение прямой параллельной оси ординат.
имеем неполное общее уравнение прямой вида Ax+C=0. Это уравнение прямой параллельной оси ординат.
При  имеем неполное общее уравнение прямой вида x=0 - уравнение координатной прямой Oy.
имеем неполное общее уравнение прямой вида x=0 - уравнение координатной прямой Oy.
Если  , то общее уравнение прямой примет вид
, то общее уравнение прямой примет вид  . Это неполное общее уравнение прямой задает прямую, проходящую через начало координат. Действительно, пара чисел
. Это неполное общее уравнение прямой задает прямую, проходящую через начало координат. Действительно, пара чисел  удовлетворяет равенству
удовлетворяет равенству  , так как
, так как  .
.
63. Угол между двумя прямыми, заданными общим уравнением. Условие параллельности и перпендикулярности.
Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
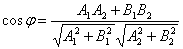
64. Уравнение прямой, проходящей через заданную точку.
Уравнение
y = y0 + k (x – x0)
называется уравнением прямой с заданным угловым коэффициентом, проходящей через данную точку.
A (x0; y0)
65. Уравнение прямой с угловым коэффициентом. Условие параллельности и перпендикулярности.
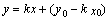 и обозначив
и обозначив  , получим
, получим
 . (2.19)
. (2.19)
(2.18), (2.19) – уравнения прямой с угловым коэффициентом. В уравнении (2.19)  – ордината точки пересечения прямой с осью
– ордината точки пересечения прямой с осью 
66. Каноническое уравнение прямой на плоскости.
Пусть  – заданная точка на прямой
– заданная точка на прямой  ,
, 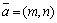 – вектор, параллельный прямой, его называют направляющим вектором прямой, и пусть
– вектор, параллельный прямой, его называют направляющим вектором прямой, и пусть  – произвольная точка прямой
– произвольная точка прямой  (рис. 22). Тогда
(рис. 22). Тогда  ,
, 
 .
.
Не нашли, что искали? Воспользуйтесь поиском:

 то
то 
 , то
, то  или
или 
 .
.