ИССЛЕДОВАНИЕ ФУНКЦИЙ

Программные вопросы

1. Область определения функции.

2. Исследование функции на четность, нечетность и периодичность.

3. Нахождение участков непрерывности функции и точки разрыва с указанием вида разрыва.

4. Точки пересечения с осями координат.

5. Асимптоты графика функции.

6. Интервалы возрастания и убывания функции.

7. Экстремумы функции.

8. Интервалы выпуклости и вогнутости и точки перегиба функции.

Решение типового примера

Пример 1.1.

Исследовать заданную функцию 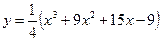методами дифференциального исчисления, начертить ее график.

Исследование функций и построение графиков рекомендуется проводить по следующей схеме:

1) найти область определения функции D(y) и исследовать функцию на непрерывность, найти точки разрыва функции, ее односторонние пределы в точках разрыва;

2) проверить четность (нечетность) функции;

3) найти точки экстремума функции и определить интервалы ее монотонности;

4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;

5) найти наклонные асимптоты графика функции;

6) построить график, используя результаты предыдущих исследований.

Решение.

1)Областью определения данной функции являются все действительные значения аргумента x, то есть , а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.

2) Исследуем функцию на четность (нечетность), для чего рассмотрим :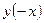

.

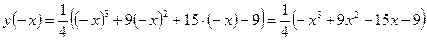Таким образом, мы видим, что 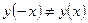. Следовательно, функция не является четной.

.

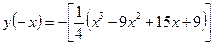Таким образом, мы видим, что 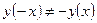. Следовательно, функция не является нечетной. Поэтому, делаем вывод, что график функции - общего вида.

3) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем ее к нулю:

, , .

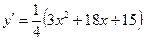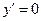
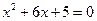Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки x ₁ = – 5, x ₂ = – 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:

x		– 5		– 1
	+		–		+
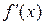
f (x)		max		min

,

.

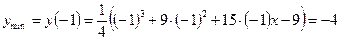4) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

, .

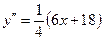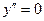
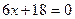
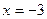Итак, функция имеет одну критическую точку 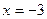. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

x		– 3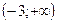
	–		+
f (x)		т. п.

Значение 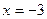является абсциссой точки перегиба графика функции, а ордината этой точки .

5) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты 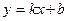воспользуемся формулами

, .

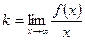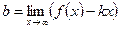Имеем

.

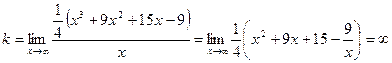Таким образом, у графика заданной функции наклонных асимптот нет.

6) Для построения графика в выбранной системе координат изобразим точки максимума , минимума , перегиба 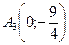. С учетом результатов предыдущих исследований построим кривую.

Не нашли, что искали? Воспользуйтесь поиском: