Решение типового примера. Пример 5.Продифференцируйте указанные функции, пользуясь правилами и формулами дифференцирования.

Пример 5. Продифференцируйте указанные функции, пользуясь правилами и формулами дифференцирования.

a) , b)

в) , г) , д) .

РЕШЕНИЕ.

а) .

Это сложная логарифмическая функция, которая дифференцируется по формуле: .

.

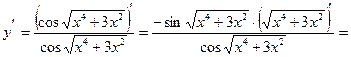
Окончательно получаем:

.

При решении использовали формулы дифференцирования:

, .

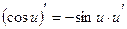б) .

Данная функция представляет собой произведение сложной показательной функции и сложной степенной функции . Воспользуемся правилом дифференцирования произведения функций: , а также формулами дифференцирования показательной и степенной функции:

, .

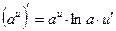Для того, чтобы закончить дифференцирование воспользуемся формулами дифференцирования сложной обратнотригонометрической и тригонометрической функций: , .

.

в) .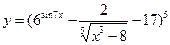

Это сложная степенная функция, которая дифференцируется по формуле: .

.

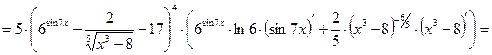
При решении использовали формулы дифференцирования:

, , .

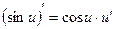г) .

Данная функция представляет собой частное сложной обратнотригонометрической функции и разности сложной показательной и степенной функций. Воспользуемся правилом дифференцирования частного , а также формулами дифференцирования:

, , .

.

д) .

Это показательно – степенная функция, которую можно продифференцировать, используя формулу

,

но эта формула сложна для запоминания, поэтому мы поступим иначе:

1. прологарифмируем обе части равенства и воспользуемся свойствами логарифмической функции

.

2. продифференцируем обе части равенства, считая сложной функцией

,

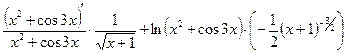Или

.

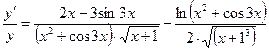3. Из полученного равенства выразим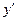

.

Не нашли, что искали? Воспользуйтесь поиском: