Задачи контрольной работы. В примерах с 6.1.1-6.1.20 исследовать заданные функции методами дифференциального исчисления, начертить их графики.

В примерах с 6.1.1-6.1.20 исследовать заданные функции методами дифференциального исчисления, начертить их графики.

6.1.1 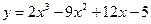.	6.1.2 .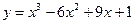
6.1.3 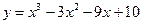.	6.1.4 .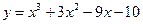
6.1.5 .	6.1.6 .
6.1.7 .	6.1.8 .
6.1.9 .	6.1.10 .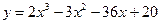
6.1.11 .	6.1.12 .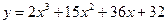
6.1.13 .	6.1.14 .
6.1.15 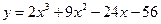.	6.1.16 .
6.1.17 .	6.1.18 .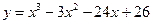
6.1.19 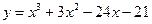.	6.1.20 .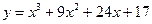

Решение типового примера

Пример 6.2.

Исследовать заданную функцию

Исследование функций и построение графиков рекомендуется проводить по следующей схеме:

1) найти область определения функции D(y)

2) исследовать функцию на непрерывность, найти точки разрыва функции, ее односторонние пределы в точках разрыва;

3) найти точки экстремума функции и определить интервалы ее монотонности;

4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;

5) найти наклонные асимптоты графика функции;

6) построить график, используя результаты предыдущих исследований.

Решение.

1) Область определения.

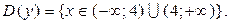
2) Исследование на непрерывность и классификация точек разрыва.

Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:

Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.

3) Исследование на экстремум и промежутки монотонности.

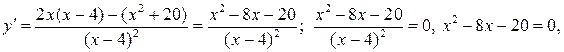
х ₁ = – 2, х ₂ = 10.

x	(– ∞, – 2)	– 2	(– 2, 4)		(4, 10)		(10, + ∞)
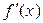
	+		–	не сущ.	–		+
f (x)		max				min

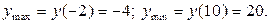
4) Исследование графика на выпуклость, вогнутость, точки перегиба.

Так как 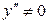, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

x	(– ∞, 4)		(4, + ∞)
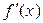
	–	не сущ.	+
f (x)

5) Исследование графика на наличие наклонных асимптот.

Таким образом, прямая 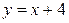– наклонная асимптота графика.

6) Построение графика.

Очевидно, график заданной функции пересекает ось Оу в точке (0; –5) и на основе обобщения результатов всех предыдущих исследований имеет вид, представленный на рис. 2.

Рис. 2

Не нашли, что искали? Воспользуйтесь поиском: