Решение типового примера. Пусть даны комплексные числа , , .

Пример 7.1.

Пусть даны комплексные числа , , .

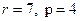а) Вычислить в алгебраической форме: , , , .

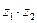б) Изобразить и в комплексной плоскости.

в) Записать в тригонометрической форме.

г) Найти и .

Решение.

а) Вычислить в алгебраической форме: , , , .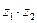

Подставим вместо и их значения и раскроем скобки:

.

Приведем подобные члены и воспользуемся определением мнимой единицы: , тогда получим

.

Вычислим . Домножим числитель и знаменатель на число, сопряженное знаменателю, т.е. на :

.

Воспользуемся определением мнимой единицы: , тогда получим:

.

Найдем :

.

Вычислим :.

.

б) Изобразить и в комплексной плоскости.

в) Записать и в тригонометрической форме.

Тригонометрическая форма записи комплексного числа имеет вид: , где , .

В нашем случае: , .

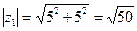Т.о. тригонометрическая форма записи комплексного числа

.

г) найти и .

Для возведения комплексного числа в степень и извлечения корней используются формулы Муавра:

,

.

Таким образом

.

.

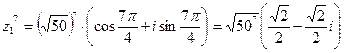Следовательно:

,

,

,

.