Задачи контрольной работы. В заданиях 4.3.1 – 4.3.20 найти указанные пределы, используя первый замечательный предел. 4.3.1 . 4.3.2 . 4.3.3 . 4.3.4 . 4.3.5

В заданиях 4.3.1 – 4.3.20 найти указанные пределы, используя первый замечательный предел.

4.3.1 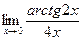.	4.3.2 .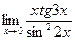
4.3.3 .	4.3.4 .
4.3.5 .	4.3.6 .
4.3.7 .	4.3.8 .
4.3.9 .	4.3.10 .
4.3.11 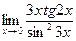.	4.3.12 .
4.3.13 .	4.3.14 .
4.3.15 .	4.3.16 .
4.3.17 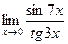.	4.3.18 .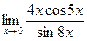
4.3.19 .	4.3.20 .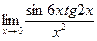

Пример 4.4. Вычислить, используя второй замечательный предел:

а) ; б) ; в) .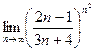

Решение.

а) .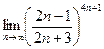

При непосредственной подстановке получаем неопределенность:

.

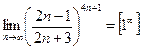В данном случае для освобождения от неопределенности будем использовать второй замечательный предел . Для этого представим основание в виде суммы единицы и некоторой бесконечно малой величины:

.

Т.о. наш предел примет вид:

.

Введем такую новую переменную , что , или . При 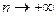переменная . Показатель степени примет вид:

.

Таким образом, пользуясь свойствами пределов и правилами действия со степенями, будем иметь:

.

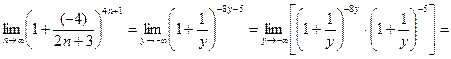
б) .

При непосредственной подстановке получаем неопределенность:

.

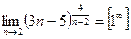В данном случае для освобождения от неопределенности будем использовать второй замечательный предел . Для этого положим , или 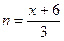, , тогда показатель степени примет вид: . При , .

Выразив основание и показатель степени через , а также воспользовавшись свойствами пределов и правилами действия со степенями, получим

.

в) .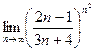

При непосредственной подстановке получаем неопределенность:

.

В данном случае для освобождения от неопределенности будем использовать второй замечательный предел . Преобразуем выражение, стоящее в скобках. Для этого представим основание в виде суммы единицы и некоторой дроби:

.

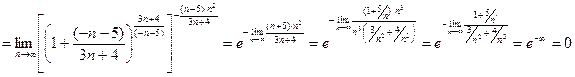Не нашли, что искали? Воспользуйтесь поиском: