Решение типового примера. Пример 12.4.1.Всхожесть семян данной партии равна 90%

Пример 12.4.1. Всхожесть семян данной партии равна 90%. Найти вероятность того, что 1) из пяти посеянных семян взойдёт не менее четырёх; 2) из 100 посеянных семян взойдет 85; 3) из 200 посеянных взойдёт не менее 190. 4) Найдите наивероятнейшее число взошедших семян из 20 посеянных.

Решение. 1) Так как вероятность того, что каждое семя прорастёт р=0,9 и семян для опыта отобрано всего 5, то вероятность того, что прорастет к семян из n посеянных можно найти по формуле Бернулли: Р_n(к)=С_n^к р^кq^n-к, где q=1-р.

В нашем случае, вероятность того, что прорастёт не менее четырех семян, находим, используя формулу Бернулли: Р₅(к≥4)= Р₅(4) + Р₅(5)=С₅⁴ р⁴q^5-4+ +С₅⁵ р⁵q^5-5= (0,9)⁴ (1- 0,9) + (0,9)⁵ 0,919. Здесь использовано, что С_n^к= С_n^n-к.

2) Так как число посеянных семян достаточно велико, то здесь необходимо использовать локальную теорему Лапласа, в соответствии с которой Р_n(к)= , где , .

Таким образом, Р₁₀₀(85)= 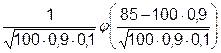= = = 0,1647=0,0549.

Значения функции находят с учётом того, что она чётная по таблице (см. приложение 1).

3) При достаточно большом числе испытаний вероятность того, что событие появится не менее к₁ и не более к₂ раз в серии из n независимых испытаний, по интегральной теореме Лапласа: Р_n (к₁ к к₂) Ф(х₂) - Ф(х₁), где Ф(х)= . Значения функции Ф(х) находятся по таблице (см. приложение 2) с учётом того, что эта функция нечётная и при х> 4 Ф(х)=0,5.

В нашем случае Р₂₀₀ (190 к 200) Ф(4,71) - Ф(-2,35) = 0,5 +0,4906= =0,9906, так как х₁= 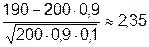, а х₂= .

4) Наивероятнейшее число 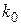наступлений события в условиях схемы Бернулли, когда вероятность появления события в каждом испытании одна и та же и равна р, а п – число испытаний, удовлетворяет условию:

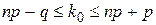, где .

В нашем случае, р =0,9, q =0,1, п =20, и , то есть, 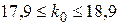, но 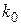- целое число. Следовательно, 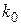=18.

Ответ: 1) 0,919; 2) 0,0549; 3) 0,9906; 4) 18.

Пример 12.4.2. Вероятность заболевания животного в стаде равна 0,002. Найдите вероятность того, что среди 1000 голов не окажется больных животных.

Решение. Поскольку вероятность заболевания животного в многочисленном стаде мала, для нахождения требуемой вероятности применим теорему Пуассона, по которой , где . В нашем случае п =1000, р =0,0002, k =0 и . Для нахождения используем таблицу (см приложение 3): 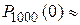0,1353.

Ответ: 0,1353.

Не нашли, что искали? Воспользуйтесь поиском: