Решение типового примера. Задача 12.6. Непрерывная случайная величина Х задана функцией распределения

Задача 12.6. Непрерывная случайная величина Х задана функцией распределения

.

Найти для неё 1) функцию плотности распределения вероятностей f(х); 2) коэффициент а; 2) вероятности попадания в интервалы (1,5; 2) и (0,5; 1,3); 3) математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. 1) Для непрерывной случайной величины по определению функции плотности вероятностей F’(х)=f(х). Следовательно,

.

2) Так как , то и , следовательно, а=1.

3) Вероятность попадания случайной величины Х в заданный интервал находится по формуле: Р(α<Х<β) = F(β) – F(α). Так как а=1, то Р(1,5<X<2)= =F(2)-F(1,5)=(2-1)² – (1,5-1)² =1 – 0,5²=0,75, а Р(0,5<X<1,3)= F(1,3) – F(0,5) = =(1,3 – 1)² – 0 = 0,09.

4) Математическое ожидание непрерывной случайной величины Х находится по формуле:

.

Так как вне интервала [1, 2] f(x)= 0 и а=1, то М(Х)= = ,

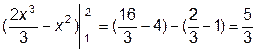Так как дисперсия непрерывной случайной величины находится по формуле , то в нашем случае

.

Среднее квадратическое отклонение случайной величины

= .

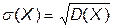Ответ: 1) 1; 2) 0,09; 3) М(Х) = , .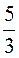

Не нашли, что искали? Воспользуйтесь поиском: