
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задачи контрольной работы. 12.7.1. Случайная величина Х равномерно распределена
12.7.1. Случайная величина Х равномерно распределена. Плотность вероятности ее f(х)=а при 1 < х < 10 и f (х)=0 при х<1 и х>10. Определить ее математическое ожидание и среднее квадратическое отклонение.
12.7.2. Равномерно распределенная случайная величина Х задана плотностью распределения 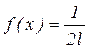 в интервале
в интервале 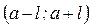 , вне этого интервала f(х)=0. Найдем математическое ожидание и дисперсию величины Х.
, вне этого интервала f(х)=0. Найдем математическое ожидание и дисперсию величины Х.
12.7.3. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной равномерно в интервале (2; 8).
12.7.4. Случайная величина Х имеет показательное распределение с параметром l=6. Написать плотность и функцию распределения этого закона.
12.7.5. Найти параметр l показательного распределения: а) заданного плотностью f(х)=0 при х<0,  при х > 0; б) заданного функцией распределения F(х)=0 при х<0 и
при х > 0; б) заданного функцией распределения F(х)=0 при х<0 и  при х > 0.
при х > 0.
2.7.6. Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью вероятностей 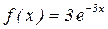 при х > 0; при х<0 f(х)=0. Найти вероятность того, что в результате испытания Х попадет в интервал (0,13; 0,7).
при х > 0; при х<0 f(х)=0. Найти вероятность того, что в результате испытания Х попадет в интервал (0,13; 0,7).
12.7.7. Непрерывная случайная величина Х распределена по показательному закону, заданному при х > 0 плотностью распределения  ; при х<0 функцией f(х)=0. Найти вероятность того, что в результате испытания Х попадет в интервал (1; 2).
; при х<0 функцией f(х)=0. Найти вероятность того, что в результате испытания Х попадет в интервал (1; 2).
12.7.8. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения 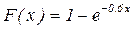 при х > 0 и F(х)=0 при х<0. Найти вероятность того, что в результате испытания Х попадет в интервал (2; 5).
при х > 0 и F(х)=0 при х<0. Найти вероятность того, что в результате испытания Х попадет в интервал (2; 5).
12.7.9. Найти математическое ожидание и дисперсию показательного распределения, заданного при х > 0: а) плотностью  ; б) функцией распределения
; б) функцией распределения 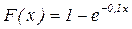 .
.
12.7.10. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности  при х > 0 и при х<0 f(х)=0.
при х > 0 и при х<0 f(х)=0.
12.7.11. Найти вероятность того, что случайная величина Х, распределенная по нормальному закону с математическим ожиданием и дисперсией равной 4, примет значение: а) в интервале (-1; 5); б) не более 8; в) не менее 5; г) в интервале (-3; 9).
12.7.12. Случайная величина Х распределена по нормальному закону. Математическое ожидание и дисперсия этой случайной величины соответственно равны 7 и 16. Найти вероятность того, что отклонение величины Х от ее математического ожидания по абсолютной величине не превзойдет двух.
12.7.13. Известно, что вес вылавливаемых в пруду карпов подчиняется нормальному закону с математическим ожиданием, равным 500 г и средним квадратическим отклонением 75 г. Определить вероятность того, что вес наудачу взятого карпа будет: а) заключен в пределах от 425 до 550 г; б) не менее 300 г; в) не более 700 г.
12.7.14. Детали по длине распределяются по нормальному закону со средним значением 20 см и дисперсией, равной 0,2 см2. Определить вероятность того, что длина наудачу взятой детали будет заключена в пределах от 19,7 см до 20,3 см, то есть отклонение в ту или иную сторону не превзойдет 0,3 см.
12.7.15. При измерении расстояний до удаленных предметов ошибка подчинена нормальному закону со средним значением, равным 20 м, и средним квадратическим отклонением 40 м. Определить вероятность того, что измеренное расстояние отклоняется от действительного в ту или другую сторону не более чем на 30 м.
12.7.16. Случайная величина подчинена нормальному закону распределения со средним квадратическим отклонением 0,4. Определить вероятность того, что значение случайной величины отклоняется от математического ожидания на величину, меньшую 0,3.
12.7.17. Средняя масса яблок – 120 г. 5% яблок данной партии отклоняются от нее более чем на 20 г. Считая, что распределение массы яблок подчиняется нормальному закону, найти, какой процент яблок имеет массу в пределах от 100 до 130 г.
12.7.18. Средняя высота дерева в некоторой роще равна 12 м. Определить, исходя из предположения, что высота деревьев распределяется по нормальному закону, какой процент деревьев имеет высоту, превышающую 15 м, если деревья, высота которых не достигает 10 м, составляет 15 %.
12.7.19. Считая, что распределение массы яблок подчинено нормальному закону с М(Х)=120 г и D(Х)=100 г2, найти вероятность того, что масса хотя бы одного из наудачу выбранных четырех яблок будет в пределах от 100 до 130 г.
12.7.20. Случайная величина, распределенная по нормальному закону, имеет математическое ожидание 5 м и дисперсию, равную 16 м2. Определить вероятность того, что случайная величина примет значение не менее 6 м и не более 8 м.
Не нашли, что искали? Воспользуйтесь поиском: