
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задачи контрольной работы
12.6.1. Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания случайная величина Х примет значение в интервале (-1,0).
12.6.2. Случайная величина Х задана функцией распределения
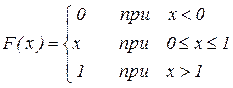
Определить вероятность того, что случайная величина Х в результате испытания примет значение, больше 0,5, но менее 0,8.
12.6.3. Случайная величина Х задана интегральной функцией распределения:

Определить вероятность того, что случайная величина примет значение в интервале:
а) (1,3; 1,5);
б) (1,2; 1,8).
12.6.4. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.5. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.6. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.7. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.8. Непрерывная случайная величина Х задана плотностью распределения:

Найти вероятность того, что Х примет значение в интервале  .
.
12.6.9. Непрерывная случайная величина задана плотностью распределения:

Найти вероятность того, что значение случайной величины Х содержится в интервале (1,3).
12.6.10. Плотность распределения вероятностей задана формулой  .
.
Найти коэффициент а и функцию распределения вероятностей случайной величины Х.
12.6.11. Случайная величина Х задана дифференциальной функцией распределения:

Определить коэффициент а.
12.6.12. Случайная величина Х задана плотностью распределения вероятностей f(х). Найти интегральную функцию распределения F(х), если

2.6.13. Случайная величина Х задана плотностью распределения вероятностей f(х). Найти интегральную функцию распределения F(х), если

12.6.14. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.15. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х), если

12.6.16. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.17. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.18. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):
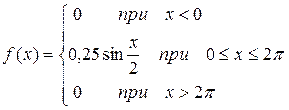
12.6.19. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.20. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):
Не нашли, что искали? Воспользуйтесь поиском: