Дифференциальные уравнения. Простейший пример дифференциального уравнения первого порядка первой степени, разрешенное относительно производной

Простейший пример дифференциального уравнения первого порядка первой степени, разрешенное относительно производной, имеет вид

.

Функция f(x) предполагается непрерывной на некотором интервале (a,b) оси x. Пользуясь другим обозначением производной, можно записать это уравнение в виде

Множество решений этого уравнения даётся формулой

(1)

где с- произвольная постоянная.

Пример 10. Найти общее решение уравнения

.

Решение. Согласно (1) имеем

Уравнения вида

(2)

называются уравнениями с разделенными переменными. Функции будем считать непрерывными.

Пример 11. Найти общее решение дифференциального уравнения

y′=0.

Решение. Перепишем его в виде

2x(1+y 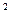)+ =0.

Домножим обе части на dx≠0 и получим

2x(1+y 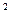)dx+ dy=0.

Это уравнение с разделяющимися переменными.

Левую и правую части полученного уравнения разделим на (1+y и проинтегрируем:

,

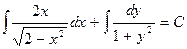arctgy-2 =C.

Пример 12. Найти общий интеграл уравнения

y′= .

Решение. Это уравнение является однородным, так как сводится к виду y′=f(

Разделим числитель и знаменатель исходной дроби на ≠0.

Получим: y′= Замена

Тогда y=x·t(x) и y′=1+x·t′.

Следовательно

t+xt′=

x· .

Разделяем переменные x,t и интегрируем:

2arctgt-3ln(t 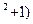=ln +c.

Возвращаясь к старым переменным y и x, получим

2 arctg 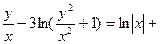c.

Не нашли, что искали? Воспользуйтесь поиском: