Контрольная работа №3. Задание 3.1. Найти неопределенные интегралы, пользуясь свойствами линейности, методами подстановки и интегрированием по частям .

Задание 3.1. Найти неопределенные интегралы, пользуясь свойствами линейности, методами подстановки и интегрированием по частям.

Задание 3.2. Вычислить несобственные интегралы.

Задание 3.3. Вычислить указанные двойные интегралы, затем переменить порядок интегрирования и сравнить ответы.

3.3.1. ,

3.3.2. ,

3.3.3. ,

3.3.4. ,

3.3.5. ,

3.3.6. ,

3.3.7. ,

3.3.8. ,

3.3.9. ,

3.3.10. ,

3.3.11. ,

3.3.12. ,

3.3.13. ,

3.3.14. ,

3.3.15. ,

.3.16. ,

3.3.17. ,

3.3.18. ,

3.3.19. ,

3.3.20. ,

3.3.21. ,

3.3.22. ,

3.3.23. ,

3.3.24. ,

3.3.25. ,

3.3.26. ,

Задание 3.4. Найти общее решение дифференциального уравнения

первого порядка.

Задание 3.5. Определить решение неоднородного дифференциального уравнения методом вариации произвольных постоянных

3.5.1. y"+y=xlnx+ ,

3.5.2. ,

3.5.3. ,

3.5.4. ,

3.5.5. ,

3.5.6.

3.5.7. ,

3.5.8. ,

3.5.9.

3.5.10.

3.5.11. ,

3.5.12. ,

3.5.13. ,

3.5.14. ,

3.5.15 ,

3.5.16. ,

3.5.17. ,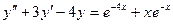

3.5.18. ,

3.5.19. ,

3.5.20. ,

3.5.21. ,

3.5.22. ,

3.5.23. ,

3.5.24. ,

3.5.25. .

3.5.26.

ТЕМА 5 [5, гл.IV]

Ряды

Составленное из чисел выражение = называется числовым рядом.

Существуют также ряды, составленные из функций, в частности, степенных функций Такие ряды называются степенными, а числа - коэффициентами степенного ряда.

С помощью признака Даламбера или радикального признака Коши находится интервал сходимости () для ряда вида . Если – общий член ряда, решается неравенство или соответственно,

Пример 13. Найти область сходимости степенного ряда

(1)

здесь .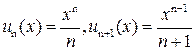

Решение. По признаку Даламбера имеем

т.к. Ряд сходится, если <1,следовательно, данный ряд сходится в интервале (- 1,1 ).

Исследуем поведение ряда на концах интервала. Положим сначала в этом ряде . Тогда ряд (1) примет вид

(2)

Ряд (2) с ходится условно в силу теоремы Лейбница [4, c.249]

При получим гармонический ряд который расходится [4, c.238].

Окончательно получим следующий интервал сходимости ряда .

Определение. Рядом Тейлора функции f(x) в точке называется степенной ряд

(1)

Теорема. Ряд Тейлора (1) в точке x функции f(x) сходится в некотором промежутке к функции f(x) в том и только в том случае, когда последовательность остаточных членов формулы Тейлора сходится к нулю в этом промежутке т.е.

f(x)= (2)

Пример 14. Разложить ln(x) в ряд Тейлора в точке x=1.

Решение. и т.

Подставляя в ряд Тейлора (2) эти величины, получим:

ln(x)=x-1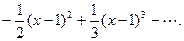

Промежуток сходимости этого ряда есть (0,2) [1].

Тема 6 [6, гл.XVII]

Ряды Фурье для функций периода 2π

Предположим, что некоторая наперёд заданная функция периода может быть разложена в тригонометрический ряд.

Итак, положим

, (1)

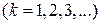где . (2)

Ряд ( 1 ), в котором коэффициенты a₀, a _к , b _к вычислены по формулам (2), называется рядом Фурье [6, c.298].

Если периодическая функция есть функция чётная, то её ряд Фурье не содержит синусов.

Если же периодическая функция нечётная, то её ряд Фурье не содержит косинусов. Поэтому для чётной функции :

(3)

Точно так же находим для нечётной функции :

(4)

Пример 15. Разложить в ряд Фурье функцию, заданную лишь на отрезке следующим равенством:

Решение. График этой функции изображен на рис.3.

рис.3

Данная функция нечётная, то ряд Фурье будет содержать лишь синусы. Для вычисления коэффициентов Фурье пользуемся формулами ( 4 ).

Идля всех.

=

Поэтомудля и для

Тема 7 [2, гл.V]

Не нашли, что искали? Воспользуйтесь поиском: