Повторение испытаний. Формула Бернулли.

Пусть проводится n независимых испытаний, в каждом из которых событие A может появиться с вероятностью p и не появиться с вероятностью q = 1 - p. Обычно первый из двух возможных исходов называют удачей, а второй — неудачей (разумеется, такое деление условно, и, возможно, кому-то захочется назвать два возможных исхода удачей и неудачей противоположным образом). Поставим задачу выяснить вероятность того, что за n испытаний произошло ровно k удач, неважно, в какой последовательности (естественно, что всегда ).При заданной последовательности удач и неудач вероятность равна (испытания независимы). Число различных способов, какими могут быть расположены k удач из n испытаний всего по формулам комбинаторики равно . По формуле для вероятности суммы несовместных событий для вероятности ровно k удач из n испытаний всего, получаем (формула Бернулли): 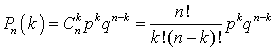.Рассмотрим несколько предельных случаев:

1) ,2) ,3) .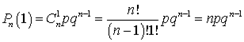

Отметим, что при фиксированном n и при малых значениях k вероятность достаточно маленькая, и это обусловлено тем, что маловероятно, что нам не повезет ни разу (не будет ни одного удачного исхода). С ростом k эта вероятность будет расти, при некотором значении достигнет максимума и далее будет убывать, становясь при k близких к n снова достаточно малой. Малое значение вероятности при k, близких к n, обусловлено тем, что маловероятно, что все испытания будут удачные.

Не нашли, что искали? Воспользуйтесь поиском: