Образец выполнения задания № 3. Задача.Дано уравнение линии в полярной системе координат

Задача. Дано уравнение линии в полярной системе координат. Надо: 1) определить точки, лежащие на линии, давая значения через промежуток, равный , начиная от в промежутке ; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.

Решение. 1) Для построения кривой, заданной уравнением , придаем значения от до через промежуток (с шагом) и заносим полученные значения в таблицу:

	0
	2,3 2,4 2,6 2,9 3,5 4,3 5,4 6,5 7 6,5 5,7 4,3 3,5 2,9 2,6 2,4 2,3

2) В полярной системе координат соединяем последовательно точки с координатами , получаем кривую (рис. 4).

3) Для получения уравнения линии в прямоугольной системе координат подставим значения полярного радиуса и угла , связывающие полярную и прямоугольную системы координат.

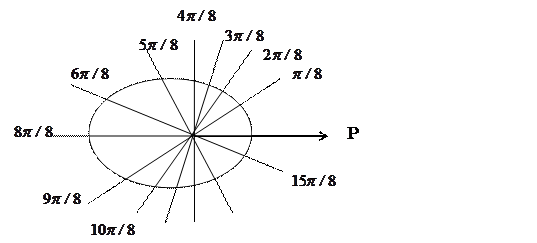
Рис. 4

, , .

Тогда .

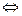
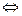
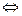
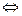
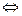
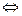
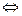
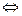
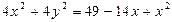
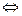
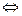
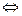
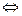
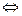
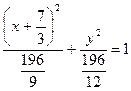- уравнение эллипса с центром в точке и полуосями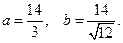

Напомним, что полярный радиус точки может принимать только неотрицательные значения.

Не нашли, что искали? Воспользуйтесь поиском: