
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение по формулам Крамера.
У данной неоднородной системы число уравнений равно числу неизвестных. Вычислим определитель этой системы:

Определитель системы не равен нулю, так что можно применить правило Крамера. Составим вспомогательный определитель  , заменив столбец коэффициентов при
, заменив столбец коэффициентов при 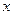 столбцом свободных членов:
столбцом свободных членов:

Вычислим определитель  , полученный из основного заменой столбца коэффициентов при переменной
, полученный из основного заменой столбца коэффициентов при переменной  столбцом свободных членов:
столбцом свободных членов:

Аналогично вычислим  :
:

По правилу Крамера: 

 Таким образом,
Таким образом, 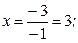


Ответ: 


Решение методом Гаусса (методом последовательного исключения неизвестных).
Запишем без изменения два первых уравнения. Умножим первое уравнение на – 2 и прибавим к третьему уравнению; запишем результат в третьей строке. Этот шаг представится в следующем виде:

Двигаемся от нижнего уравнения к верхнему и находим неизвестные:

Ответ: 
Задания к контрольной работе №1
Задание №1
Даны координаты вершин пирамиды  .Средствами векторной алгебры найти: 1) длину ребра
.Средствами векторной алгебры найти: 1) длину ребра  ; 2) площадь грани
; 2) площадь грани  ; 3) угол между ребрами
; 3) угол между ребрами  и
и  ; 4) объем пирамиды, 5) длину высоты, опущенной из вершины
; 4) объем пирамиды, 5) длину высоты, опущенной из вершины  на грани
на грани 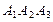
1. А1(1,3,6); А2(2,2,1); А3(-1,0,1); А4(-4,6,-3)
2. А1(-4,2,6); А2(2,-3,0); А3(-10,5,8); А4(-5,2,-4).
3. А1(7,2,4); А2(7,-1,-2); А3(3,3,1); А4(-4,2,1).
4. А1(2,1,4); А2(-1,5,-2); А3(-7,-3,2); А4(-6,-3,6).
5. А1(-1,-5,2); А2(-6,0,-3); А3(3,6,-3); А4(-10,6,7).
6. А1(0,-1,-1); А2(-2,3,5); А3(1,-5,-9); А4(-1,-6,3).
7. А1(5,2,0); А2(2,5,0); А3(1,2,4); А4(-1,1,1).
8. А1(2,-1,-2); А2(1,2,1); А3(5,0,-6); А4(-10,9,-7).
9. А1(-2,0,-4); А2(-1,7,1); А3(4,-8,-4); А4(1,-4,6).
10. А1(14,4,5); А2(-5,-3,2); А3(-2,-6,-3); А4(-2,2,-1).
11. А1(1,2,0); А2(3,0,-3); А3(5,2,6); А4(8,4,-9).
12. А1(2,-1,2); А2(1,2,-1); А3(3,2,1); А4(-4,2,5).
13. А1(1,1,2); А2(-1,1,3); А3(2,-2,4); А4(-1,0,-2).
14. А1(2,3,1); А2(4,1,-2); А3(6,3,7); А4(7,5,-3).
15. А1(1,1,-1); А2(2,3,1); А3(3,2,1); А4(5,9,-8).
16. А1(1,5,-7); А2(-3,6,3); А3(-2,7,3); А4(-4,8,-12).
17. А1(-3,4,-7); А2(1,5,-4); А3(-5,-2,0); А4(2,5,4).
18. А1(-1,2,-3); А2(4,-1,0); А3(2,1,-2); А4(3,4,5).
19. А1(4,-1,3); А2(-2,1,0); А3(0,-5,1); А4(3,2,-6).
20. А1(1,-1,1); А2(-2,0,3); А3(2,1,-1); А4(2,-2,-4).
21. А1(1,2,0); А2(1,-1,2); А3(0,1,-1); А4(-3,0,1).
22. А1(1,0,2); А2(1,2,-1); А3(2,-2,1); А4(2,1,0).
23. А1(1,2,-3); А2(1,0,1); А3(-2,-1,6); А4(0,-5,-4).
24. А1(3,10,-1); А2(-2,3,-5); А3(-6,0,-3); А4(1,-1,2).
25. А1(-1,2,4); А2(-1,-2,-4); А3(3,0,-1); А4(7,-3,1).
26. А1(0,-3,1); А2(-4,1,2); А3(2,-1,5); А4(3,1,-4).
27. А1(1,3,0); А2(4,-1,2); А3(3,0,1); А4(-4,3,5).
28. А1(-2,-1,-1); А2(0,3,2); А3(3,1,-4); А4(-4,7,3).
29. А1(-3,-5,6); А2(2,1,-4); А3(0,-3,-1); А4(-5,2,-8).
30. А1(2,-4,-3); А2(5,-6,0); А3(-1,3,-3); А4(-10,-8,7).
Задание № 2
1. Построить окружность  , проходящую через точку M (3;-3).
, проходящую через точку M (3;-3).
2. Составить уравнение окружности, диаметром которой служит отрезок прямой 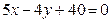 , заключенный между осями координат.
, заключенный между осями координат.
3. Найти площадь треугольника, вершина которого лежит в центре окружности  , а основание вырезано окружностью на оси абсцисс.
, а основание вырезано окружностью на оси абсцисс.
4. Через центры окружностей  и
и  проведена прямая до пересечения её с осью абсцисс. Найти угол, образованный этой прямой с осью Оx.
проведена прямая до пересечения её с осью абсцисс. Найти угол, образованный этой прямой с осью Оx.
5. Найти уравнение касательной окружностей  в точке M(1;-2).
в точке M(1;-2).
6. Найти уравнение прямой, проходящей через центр окружности 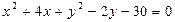 , перпендикулярной биссектрисе I и III координат углов.
, перпендикулярной биссектрисе I и III координат углов.
7. Написать уравнение эллипса, если его малая ось равна 10, а эксцентриситет  .
.
8. Найти угол между прямыми, соединяющими фокусы эллипса  с точкой пересечения прямых
с точкой пересечения прямых 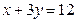 и
и  .
.
9. Определить вид кривой  и построить график.
и построить график.
10. Определить вид кривой  и построить её.
и построить её.
11. Найти уравнение геометрического места центров окружностей, касающихся оси абсцисс и проходящих через точку А(0; 3).
12. Найти уравнение геометрического места точек, каждая из которых вдвое ближе к точке А(1; 0), чем к точке В(-2; 0).
13. Найти уравнение геометрического места точек, для которых отношение расстояния до начала координат к расстоянию до прямой 3х+16=0 равно 0,6.
14. Найти уравнение геометрического места точек, каждая из которых находится вдвое дальше от точки А(3; 0), чем от оси ординат.
15. Найти уравнение геометрического места точек, равноудаленных от точки А(2; 2) и от оси абсцисс.
16. Фокусы гиперболы находятся в точках  и
и  . Гипербола проходит через точку А(2; 0). Найти уравнения ее асимптот и угол между ними.
. Гипербола проходит через точку А(2; 0). Найти уравнения ее асимптот и угол между ними.
17. На эллипсе  найти точки, в которых фокальные радиусы были бы взаимно перпендикулярны.
найти точки, в которых фокальные радиусы были бы взаимно перпендикулярны.
18. Найти параметр параболы  и уравнение ее директрисы, если известно, что эта парабола проходит через точки пересечения прямой
и уравнение ее директрисы, если известно, что эта парабола проходит через точки пересечения прямой 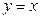 с окружностью
с окружностью  .
.
19. На гиперболе  найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.
найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.
20. Найти уравнение эллипса, у которого эксцентриситет равен 0,8, а фокальные радиусы одной из его точек равны 2 и 3, полагая, что большая ось эллипса совпадает с осью абсцисс, а центр – с началом координат.
21. Найти расстояние от правого фокуса эллипса  до прямой, проходящей через точку пересечения прямых
до прямой, проходящей через точку пересечения прямых  и
и  и центр окружности
и центр окружности  .
.
22. Найти общие точки эллипса  и окружности, проходящей через фокусы данного эллипса и имеющей центр в его верхней вершине.
и окружности, проходящей через фокусы данного эллипса и имеющей центр в его верхней вершине.
23. Написать уравнение гиперболы, симметричной относительно осей координат и проходящей через точки  и
и  .
.
24. Написать уравнение гиперболы, зная, что она симметрична относительно координат. Уравнение асимптот гиперболы  , а расстояние между фокусами
, а расстояние между фокусами  .
.
25. Написать каноническое уравнение гиперболы, зная, что расстояние одной из её вершин, лежащих на оси  , от фокусов равна 9 и 1.
, от фокусов равна 9 и 1.
26. Гипербола проходит через точку  , симметрична относительно осей координат и вещественная полуось
, симметрична относительно осей координат и вещественная полуось  . Написать уравнение перпендикуляров, опущенных из левого фокуса гиперболы на её асимптоты.
. Написать уравнение перпендикуляров, опущенных из левого фокуса гиперболы на её асимптоты.
27. Найти расстояние от центра окружности 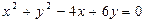 до прямой, проходящей через правый фокус гиперболы
до прямой, проходящей через правый фокус гиперболы 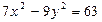 и точку
и точку  .
.
28. Построить гиперболу 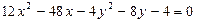 .
.
29. Составить уравнение параболы, если она проходит через точки  и
и  и симметрична относительно оси
и симметрична относительно оси  . Найти уравнение и длину перпендикуляра, опущенного из фокуса параболы на прямую, проходящую через правый фокус эллипса
. Найти уравнение и длину перпендикуляра, опущенного из фокуса параболы на прямую, проходящую через правый фокус эллипса  и точку
и точку  .
.
30. Построить параболу  . Найти координаты фокуса параболы. Написать уравнение прямой, проходящей через вершину параболы по углом
. Найти координаты фокуса параболы. Написать уравнение прямой, проходящей через вершину параболы по углом  к положительному направлению оси абсцисс.
к положительному направлению оси абсцисс.
Задание № 3
Даны уравнения линии в полярной системе координат. Надо: 1) определить точки, лежащие на линии, придавая  значения через промежуток, равный
значения через промежуток, равный  , начиная от
, начиная от  в промежутке
в промежутке  ; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.
; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 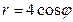
15. 
16. 
17. 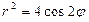
18. 
19. 
20. 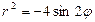
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задание № 4
Заданы уравнения прямой а и координаты точки А. Требуется найти уравнение плоскости, проходящей через точку А и через прямую а: 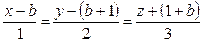 ,
,  , где b равно двум последним цифрам в номере зачётной книжки.
, где b равно двум последним цифрам в номере зачётной книжки.
Задание № 5
Заданы уравнения трех плоскостей. Требуется найти координаты точек их пересечения: 1)по формулам Крамера,
2) методом Гаусса.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17. 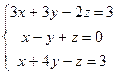 18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 
25. 
26. 
27. 
28. 
29.  30.
30. 
Не нашли, что искали? Воспользуйтесь поиском: