Образец выполнения задания № 2. Задача.Дана функция . Найдите ее градиент в точке по направлению линии : .

Задача. Дана функция . Найдите ее градиент в точке 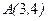по направлению линии : .

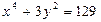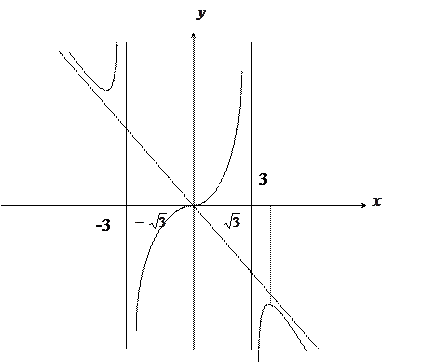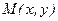Решение. Градиент функции в произвольной точке вычисляется по формуле (1).

Рис. 8

Найдем его.

Найдем эти значения в точке .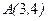

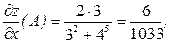
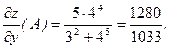
Отсюда получаем градиент в точке А по формуле (1).

Производная функции 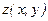в точке А по направлению вектора 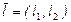вычисляется по формуле (2).

В данной задаче направлен по касательной к линии 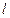в точке А (это и означает, что мы ищем производную по направлению линии , см. рис. 7).

В общем случае, когда 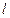имеет уравнение 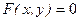, координаты касательного вектора 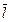в произвольной точке вычисляются по формуле

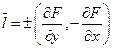
(знак 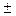соответствует тому, что в точке А можно нарисовать два противоположно – направленных касательных вектора). В нашей задаче 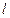: 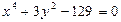, поэтому

,

, .

В точке А эти значения получаются такими .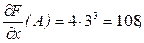

Отсюда .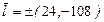

Давайте укоротим этот вектор в 12 раз; координаты остаются целыми 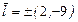, но дальнейшие вычисления упростятся. По формуле (2) получаем

.

Если мы хотим найти производную в сторону возрастания координаты х, то должно быть . В нашей задаче это получится, если у взять знак +, так как тогда , 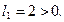Выбрав таким образом верхний знак, получим .

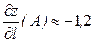Не нашли, что искали? Воспользуйтесь поиском: