
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Образцы выполнения заданий № 1-3. Задача 1.Вычислить определенные интегралы
Задача 1. Вычислить определенные интегралы
а) 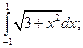 б)
б) 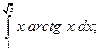 в).
в).
Решение:
а)  = [Подынтегральная функция четная] =
= [Подынтегральная функция четная] = 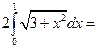
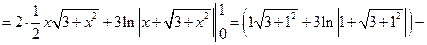
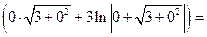
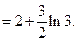
б) 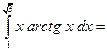 [Применив формулу интегрирования по частям] =
[Применив формулу интегрирования по частям] = 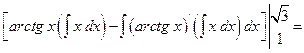

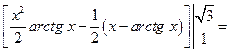

в) = [Обозначим 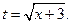 Тогда
Тогда 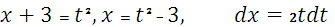 . Найдем новые пределы интегрирования:
. Найдем новые пределы интегрирования:
нижний предел при 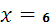 будет
будет  Верхний предел при
Верхний предел при 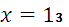 будет
будет 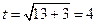 ] =
] = 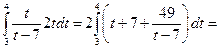
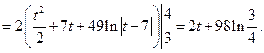
Задача 2. Вычислить несобственный интеграл или доказать его расходимость.
а) 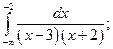 б)
б) 
Решение:
а) 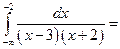 [Подынтегральная функция имеет особые точки
[Подынтегральная функция имеет особые точки 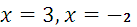 . Но они не входят в интервал интегрирования
. Но они не входят в интервал интегрирования 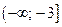 ] =
] = 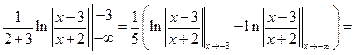
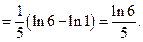
б) 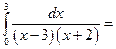 [Особая точка
[Особая точка  входит в интервал интегрирования [0; 3]] =
входит в интервал интегрирования [0; 3]] = 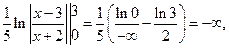 интеграл расходится.
интеграл расходится.
Задача 3. Вычислить площадь, заключенную между линиями.
Решение. Найдем абсциссы точек пересечения этих линий, решив систему.
Получим (рис. 1).
Искомая площадь равна.

Рис. 1
Задача 4. Вычислить площадь фигуры, ограниченной линией в полярных координатах.
Решение:
Графиком функции является четырехлепестковая роза. Искомая площадь равна, где - площадь одного лепестка.
Рис. 2
.
Задача 5. Найти длину линии при.
Решение:
Задача 6. Найти длину одной арки циклоиды, заданной параметрическими уравнениями.
Решение:
Когда параметр изменяется от до, получается одна из арок (рис. 3).
 .
.
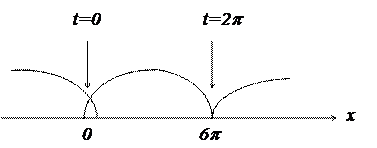
Рис. 3 Рис. 4
Задача 7. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями,,.
Решение. Когда фигура, изображенная на рис. 4, вращается вокруг оси Ох, то получится тело, объем которого.
Не нашли, что искали? Воспользуйтесь поиском: