Образец выполнения заданий № 1. Задача 1.Найти площадь фигуры, ограниченной замкнутой линией , .

Задача 1. Найти площадь фигуры, ограниченной замкнутой линией,.

Решение. Уравнение линии упростится, если перейти к полярным координатам, (- полярные координаты, - декартовы координаты). Подставив в уравнение линии, получим, - уравнение линии в полярных координатах.

Найдем допустимые значения аргумента из условия:,,,

или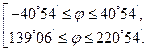

Вследствие симметрии фигуры можно найти площадь заштрихованной части и умножить на 4 (рис. 5).

Рис. 5

Задача. Вычислить двойной интеграл, используя полярные координаты.

Решение. Область интегрирования задается интервалами:

-≤x≤0, 0≤y≤

И представляет собой четверть окружности с центром в начале координат и радиуса, расположенной во второй четверти (рис. 6).

=

y=(3-x²)^1/2

D

0

Рис. 6

Перейдем к полярным координатам по формулам x=r cosφ, y=r sinφ (r, φ - полярные координаты; x, y - декартовы координаты).

Тогда область интегрирования представится в виде:

0?r? , π/2?φ?π

Заданный двойной интеграл в полярных координатах примет вид:

= .

Ответ: = .

Не нашли, что искали? Воспользуйтесь поиском: