
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЗАДАНИЯ К контрольнОЙ работЕ № 6. В задачах 1-15 вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной указанной кривой
Задача № 1.
В задачах 1-15 вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной указанной кривой, заданной уравнением в декартовых координатах. Параметр  положителен.
положителен.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6. 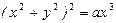 .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11. 
12. 
13. 
14. 
15. 
В задачах 16-30 вычислить двойной интеграл, используя полярные координаты.
16.  17.
17. 
18. 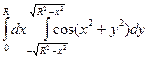 19.
19. 
20. 
21. 
22.  . 23.
. 23. 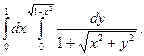
24.  25.
25. 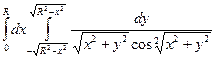
26.  27.
27. 
28.  29.
29. 
30. 
Задание №2.
В задачах 1-20 вычислить объем тела, ограниченного указанными поверхностями. Изобразить на чертеже данное тело и область интегрирования.
1. 
2. 
3. 
4. 
5. 
6.  ,
,  .
.
7. 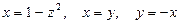 .
.
8.  .
.
9.  .
.
10. 
11. 
12. 
13. 
14. 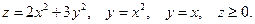
15. 
16. 
17. 
18. 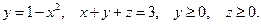
19. 
20. 
21. 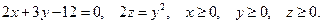
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задание № 3
1. Найти момент инерции однородного шара  массы
массы  относительно оси
относительно оси  .
.
2. Найти массу пирамиды с вершинами в точках (0; 0; 0), (1; 0; 0), (0; 1; 0) и (0; 0; 1), если плотность в точке (x, y, z) равна (x+y+z)-3.
3. Найти центр тяжести однородного тела, ограниченного конусом  и плоскостью
и плоскостью 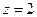 .
.
4. Найти момент инерции однородной прямой треугольной призмы массы  относительно ее бокового ребра, если все ребра равны
относительно ее бокового ребра, если все ребра равны  .
.
5. Найти массу пирамиды, ограниченной координатными плоскостями и плоскостью  , если плотность в каждой ее точке равна абсциссе этой точки.
, если плотность в каждой ее точке равна абсциссе этой точки.
6. Найти центр тяжести однородного тела, ограниченного параболоидами  и плоскостью
и плоскостью  .
.
7. Найти массу тела, ограниченного плоскостью  , цилиндром
, цилиндром  и конусом
и конусом  , если плотность в каждой его точке численно равна расстоянию от этой точки до оси
, если плотность в каждой его точке численно равна расстоянию от этой точки до оси  .
.
8. Найти момент инерции относительно оси  , ограниченной координатными плоскостями и плоскостью
, ограниченной координатными плоскостями и плоскостью  , если в каждой ее точке плотность численно равна аппликате этой точки.
, если в каждой ее точке плотность численно равна аппликате этой точки.
9. Найти центр тяжести однородного тела, ограниченного параболоидом  и плоскостью
и плоскостью  .
.
10. Найти массу тела, ограниченного координатными плоскостями и плоскостью  , если плотность в каждой его точке численно равна произведению координат этой точки.
, если плотность в каждой его точке численно равна произведению координат этой точки.
11. Найти массу однородного тела, ограниченного поверхностями  , 2y-z=0, z=0.
, 2y-z=0, z=0.
12. Найти массу однородного тела, ограниченного поверхностями
x-y-z=3, x-4=0, y=0, z=0.
13. Найти массу однородного тела, ограниченного поверхностями
x2+y-4=0, y-2z=0, z=0.
14. Найти массу однородного тела, ограниченного поверхностями
x-y+z=0, y-4=0, x=0, z=0.
15. Найти момент инерции относительно оси OZ однородного тела, ограниченного поверхности x+y-1=0, x-y-1=0, x=0, z=0, z-2=0.
16. Найти момент инерции относительно оси OZ однородного тела, ограниченного поверхности x+y=0, x-y=0, x-1=0, z=0, z=3.
17. Найти момент инерции однородного прямого параллелепипеда массы М относительно его бокового ребра, если все его ребра равны а.
18. найти момент инерции однородного шара (x-1)2+y2+z2?4R2 массы М относительно оси OX.
19. Найти массу однородного тела, ограниченного поверхностями
x2+y-2=0, 3y-2z=0, z=0.
20. Найти массу однородного тела, ограниченного поверхностями
3y+z=0, x+y=0, x-2=0, z=0.
21 Найти массу однородного тела, ограниченного поверхностями
x2+y-1=0, y-2z=0, z=0.
21. Найти массу однородного тела, ограниченного поверхностями
x-3y=0, 2x-z=0, y-2=0, z=0.
22. Найти центр тяжести однородного тела, ограниченного параболоидом x2+y2=z и плоскостью z=3.
24. Найти центр тяжести четверти окружности 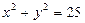 , расположенный в первом квадранте, если в каждой её точке линейная плотность пропорциональна произведению координат точки.
, расположенный в первом квадранте, если в каждой её точке линейная плотность пропорциональна произведению координат точки.
25. Найти центр тяжести однородной арки циклоида  ,
,  .
.
26. Найти центр тяжести однородной пластинки, ограниченной параболой  и осями координат.
и осями координат.
27. Найти центр тяжести однородной дуги полуокружности  , расположенный под осью OX.
, расположенный под осью OX.
28. Найти центр тяжести однородного полукруга  , расположенного под осью OX.
, расположенного под осью OX.
29. Найти центр тяжести однородной фигуры, ограниченной дугой эллипса  ,
,  и координатными осями, расположенными в I квадранте.
и координатными осями, расположенными в I квадранте.
30. Найти центр тяжести однородные фигуры, ограниченные параболами  и
и  .
.
Задача № 4
В задачах 1-30 вычислить криволинейный интеграл.
1.  , вдоль прямой линии от точки А(0;π) до точки В(π;0).
, вдоль прямой линии от точки А(0;π) до точки В(π;0).
2.  , вдоль прямой линии y=
, вдоль прямой линии y=  от точки (-1,1) до точки (2,2).
от точки (-1,1) до точки (2,2).
3.  , вдоль линии y=lnx от точки (1,0) до точки (е,1).
, вдоль линии y=lnx от точки (1,0) до точки (е,1).
4.  , вдоль дуги циклоиды x=a(t-sint), y=a(1-cost) от точки (2πа,0) до точки (4πа,0).
, вдоль дуги циклоиды x=a(t-sint), y=a(1-cost) от точки (2πа,0) до точки (4πа,0).
5.  , вдоль гипоциклоиды x=a cos3t, y=a sin3t обходя ее против часовой стрелки.
, вдоль гипоциклоиды x=a cos3t, y=a sin3t обходя ее против часовой стрелки.
6.  , вдоль параболы y=x2 от точки (-1,1) до точки (1,1).
, вдоль параболы y=x2 от точки (-1,1) до точки (1,1).
7.  , вдоль окружности
, вдоль окружности  , обходя ее против хода часовой стрелки.
, обходя ее против хода часовой стрелки.
8.  , от точки А(1,2) до точки В(3,0) вдоль ломанной линии, состоящей из отрезков прямых x=1,y=5.
, от точки А(1,2) до точки В(3,0) вдоль ломанной линии, состоящей из отрезков прямых x=1,y=5.
9.  , вдоль треугольника А(-1,0),В(1,0), С(0,1), обходя его против хода часовой стрелки.
, вдоль треугольника А(-1,0),В(1,0), С(0,1), обходя его против хода часовой стрелки.
10. 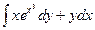 , вдоль кривой y=x2 от точки (0,0) до точки (1,1)
, вдоль кривой y=x2 от точки (0,0) до точки (1,1)
11.  , вдоль прямой АВ, А(2π,-2π); В(-2π,2π).
, вдоль прямой АВ, А(2π,-2π); В(-2π,2π).
12.  , вдоль прямой АВ, А(1,2), В(3,6)
, вдоль прямой АВ, А(1,2), В(3,6)
13.  , вдоль кубической параболы y=x3 от точки А(0,0) до точки В(1,1).
, вдоль кубической параболы y=x3 от точки А(0,0) до точки В(1,1).
14.  , вдоль ломанной АВС, А(1,2), В(3,2), С(3,5).
, вдоль ломанной АВС, А(1,2), В(3,2), С(3,5).
15.  , от точки О(0,0,0) до точки В(-2,4,5).
, от точки О(0,0,0) до точки В(-2,4,5).
16.  , вдоль дуги окружности x=Rcost, y=Rsint, О(R,0), A(0,R).
, вдоль дуги окружности x=Rcost, y=Rsint, О(R,0), A(0,R).
17.  , вдоль дуги параболы y2=x от точки О(0,0) до точки А(1,1)
, вдоль дуги параболы y2=x от точки О(0,0) до точки А(1,1)
18.  , вдоль дуги параболы y2=4-4x от точки А(1,0) до точки В(0,2)
, вдоль дуги параболы y2=4-4x от точки А(1,0) до точки В(0,2)
19.  , вдоль дуги параболы y=x2 от точки О(0,0) до точки В(1,1)
, вдоль дуги параболы y=x2 от точки О(0,0) до точки В(1,1)
20.  , вдоль дуги параболы y=x2 от точки О(0,0) до точки В(1,1)
, вдоль дуги параболы y=x2 от точки О(0,0) до точки В(1,1)
21.  , вдоль дуги астроиды x=2cos3t, y=2sin3t от точки А(2,0) до точки В(0,2)
, вдоль дуги астроиды x=2cos3t, y=2sin3t от точки А(2,0) до точки В(0,2)
22.  , вдоль дуги параболы y2=4x от точки А(0,0) до точки В(1,2)
, вдоль дуги параболы y2=4x от точки А(0,0) до точки В(1,2)
23.  , вдоль прямой АВ; А(1,0), В(0,2)
, вдоль прямой АВ; А(1,0), В(0,2)
24.  , вдоль дуги линии y=lnx от точки А(1,0) до точки В(e,1)
, вдоль дуги линии y=lnx от точки А(1,0) до точки В(e,1)
25.  , вдоль дуги параболы y=x2/4, от точки О(0,0) до точки А(2,1)
, вдоль дуги параболы y=x2/4, от точки О(0,0) до точки А(2,1)
26.  , вдоль ломанной линии y=
, вдоль ломанной линии y=  , от точки А(-1,1) до точки В(2,2)
, от точки А(-1,1) до точки В(2,2)
27. 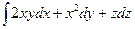 , вдоль отрезка прямой, соединяющей точки О(0,0,0) и А(2,1,-1)
, вдоль отрезка прямой, соединяющей точки О(0,0,0) и А(2,1,-1)
28.  , вдоль ломанной АВС; А(2,0), В(5,0), С(5,3)
, вдоль ломанной АВС; А(2,0), В(5,0), С(5,3)
29.  , вдоль дуги параболы y=2x2, от точки О(0,0) до точки А(1,2)
, вдоль дуги параболы y=2x2, от точки О(0,0) до точки А(1,2)
30.  , вдоль четверти дуги окружности x=Rcost, Y=Rsint, лежащей в первом квадрате и «пробегаемая» против хода часовой стрелки.
, вдоль четверти дуги окружности x=Rcost, Y=Rsint, лежащей в первом квадрате и «пробегаемая» против хода часовой стрелки.
Задание № 5
В задачах 1-30 даны функция  и вектор
и вектор  . Найти: а)
. Найти: а)  б)
б)  ; в)
; в) 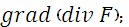 г)
г)  .
.
1.  ;
;  .
.
2.  ;
;  .
.
3.  ;
;  .
.
4.  ;
;  .
.
5.  ;
;  .
.
6.  ;
;  .
.
7. 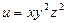 ;
;  .
.
8.  ;
;  .
.
9.  ;
;  .
.
10.  ;
; 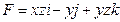 .
.
11. u=xy+xz; F=(3z2+x)i+(ex-2y)j+(2z-xy)k
12. u=xy2z; F=(4x-2y2)i+(lnz-4y)j+(x+ 
13. u=xyz3; F=(e-z-x)i+(xz+3y)j+(z+x2)k
14. u=x-2yz; F=(6x-cosy)i+(ex+z)j-(2y+3z)k.
15. u=x2yz2; F=(ez+  i+(lnz-
i+(lnz-  )j+
)j+  k.
k.
16. u=x2yz3; F=xyi+yzj+xzk.
17. u=x2z-yz2; F=3x2yi-2x2yj+(2x-1)zk.
18. u=xy+x2z; F=(y2+xz)i+(xy-z)j+(yz+x)k.
19. u=y(x+z); F=(ey+2x)i+(xz-y)j+  (exy-z)k.
(exy-z)k.
20. u=y2x-z3x2; F=(x+y  )i+(2xy+z)j+(z+sinx)k.
)i+(2xy+z)j+(z+sinx)k.
21. u=y2-z2-xz; F=(2xy2+zx)i+(exy-2xy)j-(ysinx)k.
22. u=xz+z3; F=(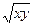 +e-x)i+(x2y2-z2)j-(4xy+z)k.
+e-x)i+(x2y2-z2)j-(4xy+z)k.
23. u=y2x2-z2y; F=7xzi+(3x+2zy)j-ex+yk.
24. u=x2-yz2; F=(6yz-cosx)i+(xey+z)j+(2xy-3yz)k.
25. u= xyz; F=(4y2z-ex)i+(3z2+x)j-(2y+3xz)k.
26. u=x2y-y2z; F=(2xy+z)i+(z-sinxy)j+(ysinx)k.
27. u=xy3z; F=(3x+2yz)i+zxyj+(e-x+ex)k.
28. u=xyz2; F=(2x2y+x)i+(xy-z)j+(y2+xz)k.
29. u=uz2-x2; F=(xz-y)i+(yz+x)j+(ey+2z)k.
30. u=xy2-z3; F=(3z2+xy)i+(ex+2z)j+(4yz-x)k
.
III семестр
теоретические вопросы
Не нашли, что искали? Воспользуйтесь поиском: