Образец выполнения заданий № 3. Задача.Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям , .

Задача. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям , .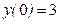

Решение. Сначала найдем общее решение , где - решение соответствующего однородного уравнения, 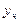- частного решение.

Составляем характеристическое уравнение и находим его корни , где - минимальная единица.

Отсюда .

Частное решение ищем в таком виде, который соответствует правой части исходного уравнения, а именно .

Чтобы найти А, В, подставим это выражение в исходное уравнение

.

Вычислив производные и упростив левую часть, получим

, отсюда будем иметь систему

, решение которой , .

Следовательно ,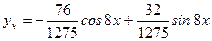

.

Производная этой функции равна

.

Подставим начальные условия: при , , 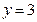. Получим

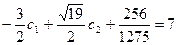, , отсюда , .

Ответ: частное решение таково

.

Не нашли, что искали? Воспользуйтесь поиском: