
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Введение в математический анализ
71-80. Найти пределы числовых последовательностей хn.
|
|  |


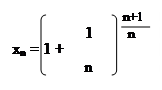
 71.
71.
 | |||||
| |||||
| |||||


 72.
72.
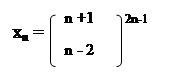 | |||
 |


 73.
73.
|





|

|
|  | ||||
 | |||||



 75.
75.
| 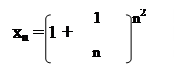 | ||||
| |||||



 76.
76.
 | |||
 |



 77.
77.
 | |||
 | |||


 78.
78.
 | |||||
 | |||||
 | |||||

 79.
79.
 | |||
 |
 80.
80.
81-90. Найти указанные пределы функций, не пользуясь правилом Лопиталя.
|
81. а) а = 2; б) а = –2; в) а = ∞
 | ||||||
 |  | |||||
|
82. а) а = 1; б) а = 2; в) а = ∞
 | |||||
 |  |

|
 | |||||
 |  | ||||
|
84. а) а = – 1; б) а = 1; с) а = ∞
 | |||||
 |
|

 | |||
|
85. а) а = 2; б) = – 2; в) а = ∞
 | |||
|


|

|
86. а) а= 1; б) а = 2; в) а = ∞
 |
|
|

|
 | |||
|
87. а) а = – 2; б) а = – 1; в) а = ∞
 | |||||
|  |


88. а) а = – 1; б) а = 1; в) а = ∞

|
|


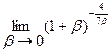
|
 89. а) а = 2; б) а = – 2; в) а = ∞
89. а) а = 2; б) а = – 2; в) а = ∞
|
|



|
90. а) а = 1; б) а = 2; в) а = ∞
 | |||
|

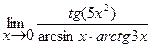 ,
, 
91-100. Функция у задается различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции у; 2) найти односторонние пределы и скачок функции в точке разрыва; 3) сделать чертеж.
 |  |
91. у = х2– 4, если х ≤ 2 92. у = 9– х2, если х ≤ 1
6–2х, если х > 2 2х+3, если х > 1
 | |||
 | |||
93. у = 4х+5, если х ≤ -1 94. у = х2+2х, если х ≤ 2
х2-4х, если х > -1 х+1, если х > 2
 |  |
95. у = 2х+3, если х ≤ -1 96. у = 4-х2, если х ≤ -2
3х-х2, если х > -1 3х + 2, если х > -2
 |  |
97. у = х2-2х, если х < 1 98. у = 4х+х2, если х < -2
1-4х, если х ≥ 1 2х+4, если х ≥ -2
 | |||
 | |||
99 у = х2+1, если х ≤ 2 100. у = х2-5, если х ≤ 1
х-3, если х > 2 1-3х, если х > 1
Не нашли, что искали? Воспользуйтесь поиском: