Применения дифференциального исчисления

141-150. Исследовать функции и построить их графики.

Исследования функций и построение графиков рекомендуется проводить по следующей схеме:

1. Найти область определения функции.

2. Исследовать на четность, нечетность, периодичность.

3. Найти точки пересечения графика функции с осями координат.

4. Исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в точках разрыва.

5. Найти точки экстремума функции и интервалы ее монотонности.

6. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции.

7. Найти асимптоты графика функции.

8. Построить эскиз графика, используя результаты предыдущих исследований.

141. а) у = 2х³ + 3х² – 36х – 21

в) у = 2sin² 2х +1, 0 £ x £ p/2

142. а) у = 2х³ + 15х² + 36 + 32

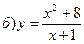в) у = –cos² 2х +2, p/4 £ x £ p/4

143. а) у = 2х³ – 15х² + 24х + 4

в) у = – ln² |х|

144. а) у = 2х³ – 9х² – 24х + 61

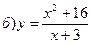в) у = e ^sinx – 2, 0 £ x £ p

145.

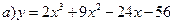
в) у = 2^cosx, – p £ x £ p

146.

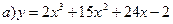
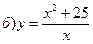в) у = – arcsin|x| + p/2, –1£ x £ 1

147.

в) у = – arccos|x| – p

148.

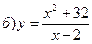в) у = – 2arctgx²

149.

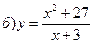в) у = – 2xsinх, p/2 £ x £ p/2

150.

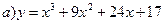
в) у = 3^–sinx, – p/2 £ x £ p

151-160. Найти наибольшее и наименьшее значения функции у = f(х) на отрезке [α; β] и написать уравнения касательной и нормали к кривой у = f(х) в точке х₀:

151. 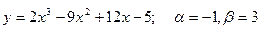, х₀=1

152. 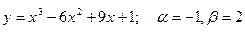, х₀=–1

153. , х₀=2

154. , х₀=–2

155. , х₀=1

156. , х₀=–1

157. , х₀=3

158. , х₀=–3

159. , х₀=1

160. , х₀=2

Не нашли, что искали? Воспользуйтесь поиском: