
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Дифференциальное исчисление функции одной переменной
|
|
101.
в) у = 2arctg х ∙arcsin 2х, г) у = lncos 6х д) 
| |||
| |||
102.
в) у = еsin х ∙ arctg 4х г) у = sinln 7х д) 
| |||
| |||
103.
|
|

 104.
104.
в) у = еarcsin х ∙ cos 4х, г) у = arctg ln 5х д) 
| |||
| |||
105.
у = 56х ∙ arcsin 5х, г) у = lnsin 7х д) 
|
| ||||
106  .
.
|
|

107.
в) у = 4tg х ∙ arctg 3х, г) у = lncos 4х д) 
|
| ||||
 108.
108.
в) у = ех² · arcsin 2х, г) у = arctg ln 5х д) 
| |||
| |||
 109.
109.
в) у = 5аrctgх · sin 4х, г) у = ln arcsin 3х д) 
|
| ||||
110.
в) у = еarcsin х · ctg 3х г) у = arctg ln 8х д) 
111-120. Найти производные второго порядка от функций:
111. у = cos3х · еsinх у = lnarctg 2x
112. у = 23х · tg2х у = cosln 5х
113. у = еtgх · ln2х у = cos 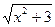
114. у = 28х · tg3х у = arcsin ln4х
115. у = еtgх · sin4х у = sin ln5х
116. у = 3ctgх · arcsin (х2) у = lnsin 6х
117. у = есtgх · cos6х у = sin ln2х
118. у = 4cosх · arctg2х у = lncos 5х
119. у = ех² · tg7х у = arcsin ln2х
120. у = 2sinх · arcsin2х у = lncos 7х
121-130. Найти производные указанного порядка от функций:
121. у(15) для у = cos5х 122. у(5) для у = (ex + e–x)/2
123. у(9) для у = sin7х 124. у(7) для у = sin(1–2х)+ 32х
125. у(83) для у = e2x 126. у(5) для у = cos7x + lnx
127. у(71) для у = 5–3x 128. у(14) для у = log5 x
121. у(5) для у = (ex – e–x)/2 122. у(11) для у = х1/2
|
|

 131. а) б)
131. а) б)

|
|
|
132. а) б)
 |  | ||||
|
в)
 | |||||
|
|
133. а) б)
 | |||||||
 | |||||||
 | |||||||
|
в)
 | |||||
|
|
134. а) б)
 |  | ||||
|
 в)
в)
|
|
 |  | ||||
|
 в)
в)
|
|
136. а) б)
 | |||||
 | |||||
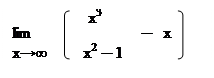 |
 в)
в)
|
|
 |  | ||||
 |

 в)
в)
|
|
138. а) б)
 |  | ||||
|
 в)
в)
|
|
139. а) б)
 |  | ||||
|
в)
 |
|
|
 |  |
|
 в)
в)
Не нашли, что искали? Воспользуйтесь поиском:


 – 7)3
– 7)3


 + 5)6,
+ 5)6,
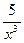 – 7)4,
– 7)4,

 – 2)4,
– 2)4,



 б) у =
cos 2х
б) у =
cos 2х
 – 1)4,
– 1)4,
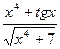
 lim
х→а
lim
х→а 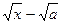
 – 1
lim
х→о √ sin вх
– 1
lim
х→о √ sin вх
