
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Опосередковані дедуктивні умовиводи
Опосередковані дедуктивні умовиводи будуються або з простих (атрибутивних чи релятивних) суджень, або зі складних суджень, або є їх комбінаціями. Розглянемо спочатку ті, що складаються лише з простих атрибутивних суджень. У свою чергу, такі умовиводи залежно від кількості засновків (двох або більше), поділяються на простий категоричний силогізм (ПКС) і складний категоричний силогізм (СКС), або полісилогізм.
А). Опосередковані дедуктивні умовиводи почав досліджувати ще Аристотель. Насамперед йому належить заслуга у виокремленні й дослідженні простого категоричного силогізму (надалі будемо записувати скорочено - ПКС). Слово "силогізм" із грецької перекладається як вивід, умовивід або міркування. Слово "категоричний" означає, що ми можемо точно визначити значення істинності суджень, з яких він складається (істина або хиба), слово "простий" означає те, що складається з простих (елементарних) суджень і є в структурному плані порівняно простим стосовно інших умовиводів.
Отже, ПКС є системою трьох взаємопов'язаних суджень виду: А (всі 8 є р), Е (всі 8 не є Р), І (деякі 8 є Р), О (деякі 8 не є Р).
Розглянемо загальну структуру ПКС:
Перший засновок (судження виду А або Е, або І, або О).
Другий засновок (судження виду А або Е, або І, або О).
Висновок (судження виду А або Е, або І, або О).
Детальне розуміння ПКС передбачає знання таких понять: термін, фігура, модус силогізму.
Під термінами ПКС розуміють суб'єкти й предикати засновків і висновку умовиводу. Для прикладу розглянемо такий силогізм:
1. Усі лауреати Нобелівської премії — видатні особистості.
2. Деякі люди — лауреати Нобелівської премії.
3. Деякі люди — видатні особистості.
Більшим терміном є предикат висновку (в нашому прикладі — слова "видатні особистості").
Меншим терміном є суб'єкт висновку (у нашому прикладі — слово "люди").
Середнім терміном є той термін, який входить лише у засновки й якого немає у висновку (у нашому прикладі — слова "лауреати Нобелівської премії").
Більшим засновком ПКС є той засновок, що містить більший термін.
Меншим засновком ПКС є той засновок, що містить менший термін.
Більший і менший засновки ПКС можна міняти місцями, що не вплине на істиннісне значення висновку.
Залежно від розташування середнього терміна розрізняють 4 фігури ПКС.
Перша фігура характеризується тим, що середній термін у ній займає місце суб'єкта в більшому засновку і місце предиката у меншому засновку.
Друга фігура характеризується тим, що середній термін у ній займає місце предиката у більшому та меншому засновках.
Третя фігура характеризується тим, що середній термін у ній займає місце суб'єкта у більшому й меншому засновках.
Четверта фігура характеризується тим, що середній термін у ній займає місце предиката у більшому засновку й місце суб'єкта у меншому засновку.
Наводимо загальну схему для всіх чотирьох фігур ПКС,
| Фігура 1 М Р 8 М | Фігура 2 Р М 8 М | Фігура 3 М Р М 8 | Фігура 4 Р М М 8 |
| 8 — Р | 8 — Р | 8 — Р | 8 — Р |
де 8 — суб'єкт висновку; Р — предикат висновку; М — середній термін.
Зі схеми ми бачимо, що висновок ПКС у всіх чотирьох фігурах залишається незмінним: 8 — Р.
Окрім фігур, виділяють і модуси (від лат. тосіия — спосіб, різновид) ПКС, тобто такі їх схеми, в яких фіксується не лише фігура, а й конкретний вид (А, Е, І або О) засновків і висновків.
Візьмемо для прикладу модус ЕІО 1. Перша літера у ньому (Е) вказує на вид більшого засновку, друга (І) — на вид меншого засновку, а третя (О) — на вид висновку. Цифра вказує на вид фігури. Наведемо приклад конкретного міркування, яке відповідало б цьому модусу.
Наведемо спочатку його схему:
1. Усі М не є Р.
2 Деякі 8 є М.
3. Деякі 8 не є Р.
Тепер підставимо замість символів конкретні значення (необхідно пам'ятати, що слово "деякі" береться не у значенні "лише деякі, а не всі", а у значенні "деякі, але, можливо, і всі"):
1. Усі мавпи не є тиграми.
2 Деякі шимпанзе є мавпами.
3. Деякі шимпанзе не є тиграми.
Аналогічно можна було б проілюструвати й інші модуси ПКС.
Висновок логічно правильного модусу ПКС є логічно достовірним за умови наявності істинних засновків. Інакше кажучи, ми гарантовано отримаємо істинний висновок у логічно правильному модусі ПКС, якщо його засновки будуть представлені істинними судженнями. Висновок у логічно неправильному модусі ПКС може бути як істинним, так і хибним, навіть якщо його засновки будуть представлені істинними судженнями.
Розглянемо для прикладу два модуси ПКС: ААА 1, ААА 2. Спробуємо визначити, який із них є логічно правильним, а який — логічно неправильним.
Розпишемо спочатку структуру модусу ААА 1, а потім підставимо замість символів конкретні значення:
1. Усі М є Р. (1. Усі вчені є людьми.)
2. Усі 8 є М. (2. Усі фізики є вченими.)
3. Усі 8 є Р. (3. Усі фізики є людьми.)
|
|

|
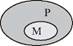
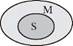
Для більшої наочності можемо подати цю структуру у вигляді кіл Ейлера.
Ми можемо побачити, що цей модус ПКС відповідає принципу побудови дедуктивних умовиводів, оскільки у ньому рух знання відбувався від загального до часткового. Отже, цей модус ПКС є логічно правильним.
Натомість модус ААА 2 є логічно неправильним. Щоб довести це положення, розпишемо його структуру й підставимо в неї конкретні значення:
1. Усі Р є М. (1. Усі фізики є людьми.)
2. Усі 8 є М. (2. Усі вчені є людьми.)
3. Усі 8 є Р. (3. Усі вчені є фізиками.)
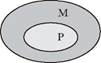
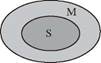
Також можемо представити схему цього модусу:
|
|

|
Ми бачимо, що висновок цього умовиводу не є логічно достовірним навіть за умови наявності істинних засновків. Він може бути як істинним, так і (переважно) хибним, залежно від того, які значення будемо підставляти у структуру замість символів. Отже, цей модус ПКС є логічно неправильним.
Логічно неправильні модуси ПКС порушують принцип побудови дедуктивних міркувань (від більш загального — до менш загального), а також правила побудови ПКС. Таких правил нараховують сім:
1. У силогізмі мають бути лише 3 (не більше і не менше) терміни.
2. Середній термін повинен бути розподілений хоча б в одному із засновків.
3. Якщо більший або менший терміни не розподілені у засновках, то вони не можуть бути розподіленими у висновку.
4. Із двох заперечних засновків неможливо зробити певного висновку.
5. Якщо один із засновків заперечний, то висновок повинен бути заперечним.
6. Із двох часткових засновків певний висновок зробити неможливо.
7. Якщо один із засновків частковий, то й висновок повинен бути частковим.
Існують 256 теоретично можливих модусів ПКС, але, як ми вже з'ясували, далеко не всі вони є логічно правильними, оскільки не відповідають принципу побудови дедуктивних міркувань (від більш загального — до менш загального), а також порушують правила побудови ПКС. Усього нараховують 24 логічно правильних модуси ПКС, 19 з яких є сильними, а 5 — слабкими. Слабкий модус відрізняється від аналогічного йому сильного тим, що в його висновку замість кванторного слова "всі" наявне кванторне слово "деякі".
Наводимо таблицю для правильних модусів ПКС, які гарантують отримання істинних висновків із істинних засновків.
| 1-а фігура ПКС | 2-а фігура ПКС | 3-я фігура ПКС | 4-а фігура ПКС | |
| Сильні модуси | ААА; ЕАЕ; АІІ; ЕІО | ЕАЕ; АЕЕ; ЕІО; АОО | ААІ; ІАІ; АІІ; ЕАО; ОАО; ЕІО | ААІ; АЕЕ; ІАІ; ЕАО; ЕІО |
| Слабкі модуси | ЕАО; ААІ | АЕО; ЕАО | АЕО |
Б). Окрім ПКС існують інші дедуктивні умовиводи, які складаються із простих атрибутивних категоричних суджень. Це складні категоричні силогізми (полісилогізми), скорочені (ентимеми) або складно-скорочені силогізми (епіхейреми і сорити).
Складним категоричним силогізмом або полісилогізмом (від грецьк. роїу — багато) називають поєднання двох або більше ПКС, у ньому висновок одного ПКС (так званого просилогізму) є одночасно засновком іншого ПКС (так званого епісилогізму).
Наприклад:
1. Усі розумні істоти повинні вміти логічно міркувати.
2. Усі люди — розумні істоти.
3. Усі люди повинні вміти логічно міркувати.
4. Усі студенти МАУП — люди.
5. Всі студенти МАУП повинні вміти логічно міркувати.
1, 2, 3 судження становлять просилогізм.
3, 4, 5 судження становлять епісилогізм.
3-тє судження одночасно є висновком просилогізму і засновком епісилогізму.
У реальних процесах міркування ПКС і полісилогізми майже не використовуються, оскільки вони є надто громіздкими. Потреба у них виникає тоді, коли ми сумніваємось у певному висновку, і для того, щоб перевірити його, розписуємо повністю все міркування. Замість ПКС і полісилогізмів частіше використовують ентимеми, епіхейреми і сорити.
Ентимема — це скорочений ПКС, в якому пропускають (але мають на увазі) один із засновків або висновок. Наприклад, маємо міркування: "Талейран був лицеміром, оскільки він був досвідченим політиком".
Це міркування є ентимемою, в якій пропущене судження-засновок, що всі досвідчені політики є лицемірами. Для того щоб перевірити ен- тимему, її необхідно розгорнути у ПКС. Якщо розгорнемо цю ентимему у ПКС, то отримаємо таке міркування:
1. Усі досвідчені політики — лицеміри.
2. Талейран був досвідченим політиком.
3. Талейран був лицеміром.
Наведене вище міркування відповідає правильному модусу ПКС (АІІ 1), тому воно також є правильним. Із ентимем будуються епіхейреми.
Епіхейрема є силогізмом, кожний із засновків якого є ентимемою.
Наприклад:
1. Захист прав людини є благородною справою, оскільки сприяє утвердженню демократії.
2. Боротьба за свободу слова є захистом прав людини, оскільки сприяє утвердженню демократії.
3. Боротьба за свободу слова є благородною справою.
У нашому прикладі в першому судженні пропущене (але мається на увазі) твердження, що всі дії, спрямовані на утвердження демократії, є благородними. У другому судженні неявно присутня думка, що все, що сприяє утвердженню демократії, є захистом прав людини.
Із простих категоричних суджень також можна побудувати так звані сорити. Сорит (від грецьк. яогоя — купа) є скороченим полі- силогізмом, у якому пропущені (але маються на увазі) деякі засновки або проміжні висновки. їх використовують тоді, коли необхідно простежити досить довгий ланцюг залежностей між класами предметів. Соритів існує багато видів, насамперед вони поділяються на прогресивні й регресивні.
Гокленівський сорит — це прогресивний полісилогізм, у якому пропущені всі більші засновки, крім першого, а також пропущені всі висновки, крім останнього. Наприклад:
1. Тварина є живою істотою.
2. Чотиринога істота є твариною.
3. Кінь є чотириногим.
4. Буцефал був конем.
5. Буцефал був живою істотою.
Аристотелівський сорит — це регресивний полісилогізм, в якому пропущені всі менші засновки й всі висновки, крім останнього.
1. Буцефал був конем.
2. Кінь є чотириногою твариною.
3. Чотиринога істота є твариною.
4. Тварина є живою істотою.
5. Буцефал був живою істотою.
В). Окрім дедуктивних умовиводів із простих атрибутивних суджень можна побудувати дедуктивні міркування й із простих релятивних суджень.
Об'єктивною підставою для таких умовиводів служить наявність одного й того самого відношення між кількома предметами (наприклад, симетричності (одночасності та ін.), кількісних (рівності та ін.), просторових тощо.
Наприклад:
1. Ельбрус вищий за Кіліманджаро.
2. Еверест вищий за Ельбрус.
3. Еверест вищий за Кіліманджаро.
Такі судження відіграють велику роль у науці й практичній життєдіяльності людей. Наприклад, у судах часто необхідно з'ясовувати, хто був початковим власником того чи іншого майна (це важливо при розподілі майна між людьми, які подали заяву на розлучення).
Не нашли, что искали? Воспользуйтесь поиском: