Уравнения с разделяющимися переменными

Определение. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде

.

Такое уравнение можно представить также в виде:

Перейдем к новым обозначениям

Получаем:

После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.

Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.

Пример. Найти общее решение дифференциального уравнения:

Интеграл, стоящий в левой части, берется по частям:

- это есть общий интеграл исходного дифференциального уравнения.

Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.

- верно

Пример. Найти решение дифференциального уравнения 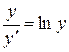при условии у(2) = 1.

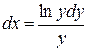
при у(2) = 1 получаем

Итого: или 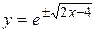- частное решение;

Проверка: , итого

- верно.

Пример. Решить уравнение

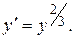
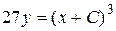- общий интеграл

- общее решение

Не нашли, что искали? Воспользуйтесь поиском: