Мәліметтерді ендіру және шығару, тағайындау операторы

Тапсырмалардың барлығында ену және шығу мәліметтері нақты типті деп қарастырылсын.

1.1 Шаршы қабырғасы а берілген. Оның периметрін [ P=4×a ] табу керек.

1.2 Шаршы қабырғасы а берілген. Оның ауданын [ S=a² ] табу керек.

1.3 Тік төртбұрыш қабырғалары a және b берілген. Оның ауданын [ S=a×b ] және периметрін [ P=2× (a+b) ] табу керек.

1.4 Шеңбер диаметрі d берілген. Оның ұзындығын табу керек: L=p×d. Мұндағы p шамасының мәнін 3.14 деп алыңыз.

1.5 Куб қырының ұзындығы a берілген. Кубтың көлемі [ V=a³ ] мен бетінің ауданын [ S=6×a² ] табу керек.

1.6 Тік параллелепипедтің қырларының ұзындықтары a, b, c берілген. Параллелепипедтің көлемі [ V=a×b×c ] мен бетінің ауданын [ S=2×(a×b+b×c+a×c)] табу керек.

1.7 R радиусы берілген шеңбердің ұзындығын [ L=2×p×R ] және осы шеңбермен шектелген дөңгелектіңауданын [ S=p×R² ] табу керек. Мұндағы p шамасының мәні 3.14- ке тең деп алынсын.

1.8 a және b сандары берілген. Олардың арифметикалық орта мәнін табу керек: (a+b)/2.

1.9 Теріс емес a және b сандары берілген. Олардың геометриялық орта мәнін, яғни олардың көбейтіндісінің квадрат түбірін табу керек: .

1.10 Нөлдік емес екі сан берілген. Олардың квадраттарының қосындысын, айырмасын, көбейтіндісін және бөліндісін табу керек.

1.11 Нөлдік емес екі сан берілген. Олардың модульдерінің қосындысын, айырмасын, көбейтіндісін және бөліндісін табу керек.

1.12 Тік бұрышты үшбұрыштың катеттері a және b берілген. Оның гипотенузасы [ ] мен периметрін [ P=a+b+c ] табу керек.

1.13 Центрлері ортақ және радиустары R₁ мен R₂ (R₁ >R₂) болатын дөңгелектер берілген. Осы дөңгелектердің аудандарын [ 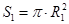, 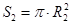] және олардың қиылысуынан пайда болған сақинаның ауданын [ S₃=S₁-S₂ ] табу керек. Мұндағы p шамасының мәні 3.14- ке тең деп алынсын.

1.14 Шеңбер ұзындығы L берілген. L=2×p×R және S=p×R² теңдіктерін пайдаланып, шеңбер радиусын және осы шеңбермен шектелетін дөңгелек ауданын табу керек. Мұндағы p шамасының мәні 3.14- ке тең деп алынсын.

1.15 Дөңгелек ауданы S берілген. L=2×p×R және S=p×R² теңдіктерін пайдаланып, дөңгелек диаметрін және осы дөңгелекті шектейтін шеңбер ұзындығын табу керек. Мұндағы p шамасының мәні 3.14- ке тең деп алынсын.

1.16 Сан осінде x₁ және x₂ координаттарымен берілген екі нүктенің ара қышықтығын анықтау керек: | x₂ - x₁ |.

1.17 Сан осінде A, B, C нүктелері берілген. AC және BC кесінділерінің ұзындықтарын және олардың қосындысын табу керек.

1.18 Сан осінде A, B, C нүктелері берілген. C нүктесі А және B нүктелерінің арасында орналасқан. АС және ВС кесінділерінің көбейтіндісін табу керек.

1.19 Тік төртбұрыштың қарама-қарсы төбелерінің координаттары берілген: (x₁, y₁), (x₂, y₂). Тік төртбұрыштың қабырғалары координат осьтеріне параллель. Берілген тік төртбұрыштың периметрі мен ауданын табу керек.

1.20 Жазықтықта координаттарымен берілген (x₁, y₁), (x₂, y₂) нүктелерінің ара қашықтығын табу керек. Ара қашықтықты табу формуласы: .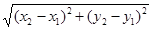

1.21 Жазықтықтағы үшбұрыш төбелері координаттарымен берілген (x₁, y₁), (x₂, y₂), (x₃, y₃). Жазықтықтағы екі нүктенің ара қашықтығын табу формуласын пайдаланып (20-есепті қараңыз) үшбұрыштың периметрі мен ауданын табу керек. Қабырғалары a, b, c үшбұрыштың ауданын есептеуге Герон формуласын пайдаланыңыз: , мұндағы p=(a+b+c)/2 – жарты периметр.

1.22 a және b айнымалыларының мәндерін ауыстырып, a мен b -ның жаңа мәндерін шығару керек.

1.23 a,b,с айнымалылары берілген. Олардың мәндерін келесі тәртіппен ауыстырып, алынған жаңа мәндерді шығару керек: а -ны b -ға, b -ны c -ға, c -ны a -ға.

1.24 a,b,с айнымалылары берілген. Олардың мәндерін келесі тәртіппен ауыстырып, алынған жаңа мәндерді шығару керек: а -ны c -ға, c -ны b -ға, b -ны a -ға.

1.25 Мәні берілген х үшін y=3x⁶ – 6x² – 7 функциясының мәнін есептеу керек.

1.26 Мәні берілген х үшін y=4(x – 3)⁶ – 7(x – 3)³ + 2 функциясының мәнін есептеу керек.

1.27 а саны берілген. Қосымша айнымалыны және үш рет көбейту амалын пайдаланып а⁸ мәнін есептеу керек. Ол үшін рет-ретімен а², а⁴ және а⁸ мәндерін есептеңіз де, а -ның барлық дәрежелерін шығарыңыз.

1.28 а саны берілген. Қосымша айнымалыны және бес рет көбейту амалын пайдаланып а¹⁵ мәнін есептеу керек. Ол үшін рет-ретімен а², а³, а⁵, а¹⁰ және а¹⁵ мәндерін есептеңіз де, а -ның барлық дәрежелерін шығарыңыз.

1.29 бұрышының мәні градуспен берілген (0< <360). 180°=p× радиан екенін ескеріп, берілген бұрыштың мәнін радиан арқылы есептеу керек. Мұндағы p шамасының мәнін 3.14 деп алыңыз.

1.30 бұрышының мәні радианмен берілген (0< <2×p). 180°=p× радиан екенін ескеріп, берілген бұрыштың мәнін градус арқылы есептеу керек. Мұндағы p шамасының мәнін 3.14 деп алыңыз.

1.31 Т температурасы Фаренгейт градусымен берілген. Осы температура мәнін Цельсий градусымен анықтау керек. Цельсий бойынша Т_С температурасы Фаренгейт бойынша T_F температурасымен келесі қатынас бойынша байланысқан: Т_С=(T_F - 32)×5/9.

1.32 Т температурасы Цельсий градусымен берілген. Осы температура мәнін Фаренгейт градусымен анықтау керек. Цельсий бойынша Т_С температурасы Фаренгейт бойынша T_F температурасымен келесі қатынас бойынша байланысқан: Т_С=(T_F - 32)×5/9.

1.33 x кг конфеттің бағасы а тг екені белгілі.Салмағы 1 кг және у кг осындай конфеттің құны қанша екенін анықтау керек.

1.34 x кг шоколадты конфеттің бағасы а тг және y кг иристің бағасы b тг екені белгілі.Салмағы 1 кг шоколадты конфет пен 1 кг иристің құны қанша екенін және шоколадты конфеттің бағасы иристің бағасынан неше есе артық екенін анықтау керек.

1.35 Қозғалыссыз судағы қайық жылдамдығы V км/сағ, өзен ағысының жылдамдығы U км/сағ (U<V). Қайықтың көлдегі қозғалыс уақыты Т₁ сағ, ал өзен бойымен (ағысқа қарсы) – T₂ сағ. Қайықтың жүрген жолы S -ті анықтау керек (жол = уақыт × жылдамдық). Ағысқа қарсы қозғалған кезде қайықтың жылдамдығы ағыс жылдамдығына тең шамаға кемитінін ескеру керек.

1.36 Бірінші автокөліктің жылдамдығы V₁ км/сағ, екіншісінікі – V₂ км/сағ және олардың ара қашықтығы S км. Егер автокөліктер біріне-бірі жақындау бағытында қозғалса, онда олардың ара қашықтығы Т сағаттан соң неге тең? Бұл қашықтық бастапқы қашықтық пен автокөліктер жүрген жалпы жолдың айырымының модуліне тең; (жалпы жол = уақыт × қосынды жылдамдық).

1.37 Бірінші автокөліктің жылдамдығы V₁ км/сағ, екіншісінікі – V₂ км/сағ және олардың ара қашықтығы S км. Егер автокөліктер бір-бірінен алыстау бағытында қозғалса, онда олардың ара қашықтығы Т сағаттан соң неге тең? Бұл қашықтық бастапқы қашықтық пен автокөліктер жүрген жалпы жолдың айырымының модуліне тең; (жалпы жол = уақыт × қосынды жылдамдық).

1.38 a×x+b=0 сызықтық теңдеуінің a және b коэффициенттері берілген. Оның шешімін табу керек (а – 0-ден өзге сан).

1.39 a×x²+b×x +c=0 квадрат теңдеуініңкоэффициенттері a, b және с берілген (а – 0-ден өзге сан) және теңдеу дискримананты оң сан екені белгілі болса, онда теңдау түбірлерін табу керек. Анықталған түбірлердің алдымен кішісін, сонан соң үлкенін шығару керек. Квадрат теңдеу түбірлері келесі өрнек арқылы анықталады: , мұндағы d=b²-4×a×c.

1.40 Коэффициенттері a₁,b₁,c₁,a₂,b₂,c₂ арқылы берілген және алдын-ала жалғыз шешімі бар екені белгілі. Келесі сызықтық теңдеулер жүйесін шешу керек:

a₁× x+b₁× y=c_1,

a₂× x+b₂× y=c₂.

Ол үшін келесі формулаларды пайдаланыңыз:

x=(c₁×b₂-c₂×b₁)/d, y=(a₁×c₂-a₂×c₁)/d, d=a₁×b₂-a₂×b₁.

Бүтін сандар

Бұл бөлімдегі есептердің барлығындағы ену/шығу мәндері бүтін сандар болып табылады. Цифрларының саны көрсетілген сандардың барлығы (екі таңбалы сан, үш таңбалы сан, т.т.) оң мәнді деп есептеледі.

2.1. L қашықтығы сантиметрмен берілген. Бүтін бөлу амалын (div) пайдаланып, ондағы толық метрлер санын анықтау керек (1 м = 100 см).

2.2. М салмағы килограммен берілген. Бүтін бөлу амалын (div) пайдаланып, ондағы толық тонналар санын анықтау керек (1 т = 1000 кг).

2.3. Файл өлшемі байтпен берілген. Бүтін бөлу амалын (div) пайдаланып, осы файлдағы толық килобайттар санын анықтау керек (1 килобайт = 1024 байт).

2.4. Оң бүтін a және b сандары берілген (a>b). a ұзындықты кесіндіде b ұзындықты кесінділердің барынша көп саны орналасқан (бірінің үстіне бірі орналаспаған). Бүтін бөлу амалын (div) пайдаланып, а кесіндісіндегі b кесінділерінің санын анықтау керек.

2.5. Оң бүтін a және b сандары берілген (a>b). a ұзындықты кесіндіде b ұзындықты кесінділердің барынша көп саны орналасқан (бірінің үстіне бірі орналаспаған). Бүтін бөлудің қалдығын алу амалын (mod) пайдаланып, а кесіндісінің қолданылмаған бөлігінің ұзындығын анықтау керек.

2.6. Екі таңбалы сан берілген. Алдымен оның сол цифрын (ондығын), сосын оң цифрын (бірлігін) шығару керек. Ондықты – бүтін бөлу амалын (div), ал бірлікті – бүтін бөлудің қалдығын алу амалын (mod) пайдаланып табу керек.

2.7. Екі таңбалы сан берілген. Оның цифрларының қосындысы мен көбейтіндісін табу керек.

2.8. Екі таңбалы сан берілген. Оның цифрларының орнын алмастыру арқылы алынған санды шығару керек.

2.9. Үш таңбалы сан берілген. Бүтін бөлу амалын бір рет пайдаланып, оның бірінші цифрын (жүздігін) табу керек.

2.10. Үш таңбалы сан берілген. Алдымен, оның ең соңғы цифрын (бірлігін), сонан соң ортадағы цифрын (ондығы) табу керек.

2.11. Үш таңбалы сан берілген. Оның цифрларының қосындысы мен көбейтіндісін табу керек.

2.12. Үш таңбалы сан берілген. Оның цифрларын оңнан солға қарай оқыған кезде пайда болатын санды шығару керек.

2.13. Үш таңбалы сан берілген. Оның сол шетіндегі бірінші цифрын қиып алып, соңына (оң шетіне) орналастырды. Пайда болған санды шығару керек.

2.14. Үш таңбалы сан берілген. Оның оң шетіндегі соңғы цифрын қиып алып, басына (сол шетіне) орналастырды. Пайда болған санды шығару керек.

2.15. Үш таңбалы сан берілген. Оның жүздігі мен ондығының орнын алмастырып (мысалы, 123 берілген болса, онда нәтижелік сан 213 болады), пайда болған санды шығару керек.

2.16. Үш таңбалы сан берілген. Оның бірлігі мен ондығының орнын алмастырып (мысалы, 123 берілген болса, онда нәтижелік сан 132 болады), пайда болған санды шығару керек.

2.17. 999-дан артық бүтін сан берілген. Бүтін бөлу және бүтін бөлудің қалдығын алу амалдарын бір реттен пайдаланып, берілген сандағы жүздікке сәйкес келетін цифрды анықтау керек.

2.18. 999-дан артық бүтін сан берілген. Бүтін бөлу және бүтін бөлудің қалдығын алу амалдарын бір реттен пайдаланып, берілген сандағы мыңдыққа сәйкес келетін цифрды анықтау керек.

2.19. Тәулік басынан бері N секунд өтті (N – бүтін сан). Тәулік басынан бері өткен толық минуттар санын анықтау керек.

2.20. Тәулік басынан бері N секунд өтті (N – бүтін сан). Тәулік басынан бері өткен толық сағаттар санын анықтау керек.

2.21. Тәулік басынан бері N секунд өтті (N – бүтін сан). Соңғы минут басталған соң өткен секундтар санын анықтау керек.

2.22. Тәулік басынан бері N секунд өтті (N – бүтін сан). Соңғы сағат басталған соң өткен секундтар санын анықтау керек.

2.23. Тәулік басынан бері N секунд өтті (N – бүтін сан). Соңғы сағат басталған соң өткен толық минуттар санын анықтау керек.

2.24. Апта күндері былай нөмірленген: 0 – жексенбі, 1 – дүйсенбі, 2 – сейсенбі,... 6 – сенбі. 1-365 аралығындағы K саны берілген. Егер жылдың 1 қаңтары дүйсенбіге сай келсе, онда жылдың K-шы күні аптаның қай күніне сай келетінін анықтау керек.

2.25. Апта күндері былай нөмірленген: 0 – жексенбі, 1 – дүйсенбі, 2 – сейсенбі,... 6 – сенбі. 1-365 аралығындағы K саны берілген. Егер жылдың 1 қаңтары бейсенбіге сай келсе, онда жылдың K-шы күні аптаның қай күніне сай келетінін анықтау керек.

2.26. Апта күндері былай нөмірленген: 0 – жексенбі, 1 – дүйсенбі, 2 – сейсенбі,... 6 – сенбі. 1-365 аралығындағы K саны берілген. Егер жылдың 1 қаңтары сейсенбіге сай келсе, онда жылдың K-шы күні аптаның қай күніне сай келетінін анықтау керек.

2.27. Апта күндері былай нөмірленген: 0 – жексенбі, 1 – дүйсенбі, 2 – сейсенбі,... 6 – сенбі. 1-365 аралығындағы K саны берілген. Егер жылдың 1 қаңтары сенбіге сай келсе, онда жылдың K-шы күні аптаның қай күніне сай келетінін анықтау керек.

2.28. Апта күндері былай нөмірленген: 1 – дүйсенбі, 2 – сейсенбі,... 6 – сенбі, 7 – жексенбі. 1-365 аралығындағы K саны және 1-7 аралығындағы N саны берілген. Егер жылдың 1 қаңтары N-ге сай келсе, онда жылдың K-шы күні аптаның қай күніне сай келетінін анықтау керек.

2.29. Оң бүтін a,b,c сандары берілген. Өлшемі a´b тік төртбұрыштың ішінде қабырғасы с-ға тең шаршылардың максимум саны орналасқан. Тік төртбұрыштың ішінде орналасқан шаршылардың саны мен бос қалған бөлігінің ауданын анықтау керек.

2.30. Қандай да бір жылдың нөмірі берілген (оң бүтін сан). Оған сай келетін жүзжылдықтың нөмірін анықтау керек. Мысалы, 20-шы жүзжылдықтың басы 1901 жыл деп есептелсін.

Не нашли, что искали? Воспользуйтесь поиском: