
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Б) Функциялар пен процедураларға қосымша тапсырмалар
9.37. ab шамасын ab=exp(b× ln(a)) формуласымен есептейтін нақты типті Power(a,b) функциясын сипаттау керек (a,b параметрлері нақты). a≤0 жағдайда функция 0-дік мән қайтарады. Осы функцияны пайдаланып, мәндері берілген a,b,c,p шамалары үшін ap,bp,cp дәрежелері есептелінсін.
9.38. an шамасын келесі формулалармен есептейтін нақты типті Power2(a,n) функциясын сипаттау керек:
a0=1,
an=a×a×…× a (көбейткіштер саны n), егер n>0 болса,
an=1/(a×a×…× a) (көбейткіштер саны | n |), егер n<0 болса.
(a – нақты, b – бүтін параметр). Осы функция көмегімен мәндері берілген
a,m,n,k шамалары үшін am,an,ak дәрежелері есептелінсін.
9.39. Осы бөлімнің 37-ші және 38-ші есептеріндегі Power және Power2 функцияларын пайдалана отырып, ab шамасын анықтауға арналған Power3(a,b) функциясы сипатталсын. Бұл функция арқылы ab шамасы былай есептелінсін: егер b -ның бөлшек бөлігі нөлдік болса, онда Power2(a,Round(b)) функциясы орындалады, әйтпесе Power(a,b) функциясы шақырылады. Осы функцияны пайдаланып, мәндері берілген a,b,c,p шамалары үшін ap,bp,cp дәрежелері есептелінсін.
9.40. exp(x) функциясының жуық мәнін келесі қосынды көмегімен есептейтін нақты типті Exp1(x,ε) функциясын сипаттау керек(x,ε – нақты параметрлер, ε>0):
exp(x)=1+x+x2/(2!)+ x3/(3!)+…+ xn/(n!)+…
(n!=1× 2× 3× …× n). Қосындыда ε- нан үлкен барлық қосылғыштарды ескеру керек. Exp1 функциясының көмегімен мәні берілген х пен алты түрлі мәні берілген ε үшін экспонентаның жуық мәндері есептелінсін.
9.41. sin(x) функциясының жуық мәнін келесі қосынды көмегімен есептейтін нақты типті Sin1(x,ε) функциясын сипаттау керек (x,ε – нақты параметрлер, ε>0):
sin(x)=x – x3/(3!)+ x5/(5!) – …+(-1) n× x2× n+1/((2× n+1)!)+…
Қосындыда модулі ε- нан үлкен барлық қосылғыштарды ескеру керек. Sin1 функциясының көмегімен мәні берілген х пен алты түрлі мәні берілген ε үшін синустың жуық мәндері есептелінсін.
9.42. cos(x) функциясының жуық мәнін келесі қосынды көмегімен есептейтін нақты типті Cos 1(x,ε) функциясын сипаттау керек (x,ε – нақты параметрлер, ε>0):
cos(x)=1 – x2/(2!)+ x4/(4!) – …+(-1) n× x2× n/((2× n)!)+…
Қосындыда модулі ε- нан үлкен барлық қосылғыштарды ескеру керек. Cos1 функциясының көмегімен мәні берілген х пен алты түрлі мәні берілген ε үшін синустың жуық мәндері есептелінсін.
9.43. Ln(x+1) функциясының жуық мәнін келесі қосынды көмегімен есептейтін нақты типті Ln1(x,ε) функциясын сипаттау керек (x,ε – нақты параметрлер, | x |<1, ε>0):
Ln(x+1)=x – x2/2+ x3/3 – …+(-1) n× x n+1/(n+1)+…
Қосындыда модулі ε- нан үлкен барлық қосылғыштарды ескеру керек. Ln1 функциясының көмегімен мәні берілген х пен алты түрлі мәні берілген ε үшін Ln(x+1) функциясының жуық мәндері есептелінсін.
9.44. arctg(x) функциясының жуық мәнін келесі қосынды көмегімен есептейтін нақты типті Arctg1(x,ε) функциясын сипаттау керек (x,ε – нақты параметрлер, | x |<1, ε>0):
arctg(x)=x – x3/3+ x5/5 – …+(-1) n× x2× n+1/(2× n+1)+…
Қосындыда модулі ε- нан үлкен барлық қосылғыштарды ескеру керек. Arctg1 функциясының көмегімен мәні берілген х пен алты түрлі мәні берілген ε үшін arctg(x) функциясының жуық мәндері есептелінсін.
9.45. (1+x)a функциясының жуық мәнін келесі қосынды көмегімен есептейтін нақты типті Power4(x,a,ε) функциясын сипаттау керек (x,a,ε – нақты параметрлер, | x |<1; a,ε>0):
(1+x)a=1+a× x + a× (a – 1)× x2/(2!)+ …+ a× (a – 1)× … × (a – n+1)× xn/(n!)+…
Қосындыда модулі ε- нан үлкен барлық қосылғыштарды ескеру керек. Power4 функциясының көмегімен мәні берілген х пен алты түрлі мәні берілген ε үшін (1+x)a функциясының жуық мәндері есептелінсін.
9.46. Келесі Евклид алгоритмін қолданып, оң a және b бүтін сандарының ең үлкен ортақ бөлгішін (ЕҮОБ) табатын NOD2(a,b) функциясын сипаттау керек:
ЕҮОБ(a,b)= ЕҮОБ(b, a mod b), егер b ≠ 0 болса; ЕҮОБ(a,0)=а.
Сипатталған функция көмегімен мәндері берілген бүтін a,b,c,d сандары
үшін (a,b), (a,c), (a,d) жұптарының ЕҮОБ-тері анықталсын.
9.47. NOD2 функциясын пайдалана отырып (9.46-есеп), a/b бөлшегін қасқартылмайтын p/q бөлшегіне түрлендіретін Frac1(a,b,p,q) функциясын сипаттау керек (a,b – ену параметрлері, p,q – шығу параметрлері, барлығы бүтін типті). Нәтижелік p/q бөлшегінің таңбасы оның алымына тіркеледі, (яғни q>0). Frac1 функциясын қолданып, мәндері берілген бүтін a,b,c,d,e,f,g,h үшін a/b+c/d, a/b+e/f, a/b+g/h өрнектеріне тең қысқартылмайтын бөлшектер табылсын.
9.48. a және b бүтін сандарының ең кіші ортақ еселігі (ЕКОЕ) келесі формула көмегімен анықталатынын ескере отырып және 9.46-есептегі NOD2 функциясын қолдана отырып, a және b бүтін сандарының ең кіші ортақ еселігін табатын NOK2(a,b) бүтін функциясын сипаттау керек. Сипатталған функция көмегімен мәндері берілген бүтін a,b,c,d сандары үшін (a,b), (a,c), (a,d) жұптарының ЕКОЕ-тері анықталсын.
9.49. ЕҮОБ(a,b,c)= ЕҮОБ(ЕҮОБ(a,b),c) қатынасын және 9.46-есептегі NOD2 функциясын қолдана отырып, a, b және с бүтін оң сандарының ең үлкен ортақ бөлгішін табатын NOD3(a,b,c) бүтін функциясын сипаттау керек. Осы функцияны қолданып, мәндері берілген a,b,c,d шамалары үшін (a,b,c), (a,c,d), (b,c,d) үштіктерінің ЕҮОБ-рі анықталсын.
9.50. Секундпен берілген t уақыты бойынша ондағы сағат (h), минут (m) және секунд (s) көлемін анықтайтын TimeToHMS(t,h,m,s) процедурасын сипаттау керек (t – ену параметрі, h,m,s – әрі ену, әрі шығу параметрлері, барлығы оң бүтін сандар). Осы процедураны пайдаланып, t1,t2,…,t5 уақыт аралығындағы сағат (h), минут (m) және секунд (s) көлемі анықталсын.
9.51. Сағат (h), минут (m) және секунд (s) арқылы берілген уақытты t секундқа арттыратын IncTime(h,m,s,t) процедурасын сипаттау керек (t – ену параметрі, h,m,s – әрі ену, әрі шығу параметрлері, барлығы оң бүтін сандар). Бүтін t шамасы және қандай да бір уақыт аралығы сағат (h), минут (m) және секунд (s) арқылы берілген. IncTime процедурасының көмегімен берілген уақыт t секундқа арттырылсын және h,m,s- тің жаңа мәндері шығарылсын.
9.52. Оң бүтін y саны кібісе жылға сәйкес келсе (ақпанда 29 күн болса) – TRUE, әйтпесе – FALSE мәнін қайтаратын логикалық IsLeapYear(y) функциясын сипаттау керек. у параметрінің бес мәні үшін IsLeapYear функциясы орындалсын. Кібісе жылдың белгісі – 4-ке қалдықсыз бөлінеді (100-ге бөлінетін және 400-ге бөлінбейтіндерінен басқасы).
9.53. IsLeapYear функциясын пайдаланып (9.52-есеп), у -ші жылдың m -ші айындағы күндер санын анықтайтын бүтін MonthDays(m,y) функциясын сипаттау керек (1≤m≤12, y>0). Берілген у жылы мен m1,m2,m3 айлары үшін MonthDays функциясының мәндері табылсын.
9.54. MonthDays функциясын пайдаланып (9.53-есеп), күн (d), ай (m) және жылды (y) қамтитын дұрыс мәлімет бойынша осы күннен алдыңғы күнді анықтайтын PrevDate(d,m,y) процедурасын сипаттау керек (d,m,y – әрі ену, әрі шығу параметрлері, барлығы бүтін типті). Сипатталған процедура үш күнге қолданылсын және олардың алдындағы күндер шығарылсын.
9.55. MonthDays функциясын пайдаланып (9.53-есеп), күн (d), ай (m) және жылды (y) қамтитын дұрыс мәлімет бойынша осы күннен кейінгі күнді анықтайтын NextDate(d,m,y) процедурасын сипаттау керек (d,m,y – әрі ену, әрі шығу параметрлері, барлығы бүтін типті). Сипатталған процедура үш күнге қолданылсын және олардан кейінгі күндер шығарылсын.
9.56. Ұштарының координаттары арқылы берілген АВ кесіндісінің ұзындығын анықтайтын нақты типті Leng(xa,ya,xb,yb) функциясын сипаттау керек (xa,ya,xb,yb – нақты параметрлер). Кесінді ұзындығы келесі формула көмегімен анықталады: 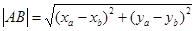 . Егер A,B,C,D нүктелерінің координаттары берілген болса, онда AB, АC, АD кесінділерінің ұзындықтары анықталсын.
. Егер A,B,C,D нүктелерінің координаттары берілген болса, онда AB, АC, АD кесінділерінің ұзындықтары анықталсын.
9.57. Leng функциясын пайдаланып (9.56-есеп), төбелерінің координаттары арқылы берілген АВС үшбұрышының периметрін есептейтін нақты типті Perim(xa,ya,xb,yb,xc,yc) функциясын сипаттау керек (xa,ya,xb,yb,xc,yc – нақты параметрлер). Егер A,B,C,D нүктелерінің координаттары берілген болса, онда ABC, АCD, АBD үшбұрыштарының периметрі анықталсын.
9.58. Leng және Perim функцияларын пайдаланып (9.56 және 9.57-есептер), төбелерінің координаттары арқылы берілген АВС үшбұрышының ауданын есептейтін нақты типті Area(xa,ya,xb,yb,xc,yc) функциясын сипаттау керек (xa,ya,xb,yb,xc,yc – нақты параметрлер). Үшбұрыш ауданы келесі формула арқылы анықталады:
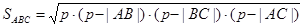 ,
,
мұндағы р – жарты периметр. Егер A,B,C,D нүктелерінің координаттары
берілген болса, онда ABC, АCD, АBD үшбұрыштарының ауданы анық-
талсын.
9.59. Leng және Area функцияларын пайдаланып (9.56 және 9.58-есептер), Р(xp,yp) нүктесінен АВ кесіндісіне дейінгі қашықтығын (d=2×SPAB/|AB|, мұндағы SPAB – PAB үшбұрышының ауданы) есептейтін нақты типті Dist(xp,yp,xa,ya,xb,yb) функциясын сипаттау керек. Егер Р,A,B,C нүктелерінің координаттары берілген болса, онда Р нүктесінен AB, АC, BС кесінділеріне дейінгі қашықтықтар анықталсын.
9.60. Dist функциясын пайдаланып (9.59-есеп), төбелерінің координаттары арқылы берілген АВС үшбұрышының А, В және С төбелерінен түсірілген hA,hB,hC биіктіктерін есептейтін Heights(xa,ya,xb,yb,xc,yc,hA,hB,hC) процедурасын сипаттау керек. Егер A,B,C,D нүктелерінің координаттары берілген болса, онда ABC, АCD, АBD үшбұрыштарының барлық биіктіктері анықталсын.
Не нашли, что искали? Воспользуйтесь поиском: