Таңдау операторы

5.1. 1-7 аралығындағы бүтін сан берілген. Берілген санға сай келетін апта күнінің атауын шығару керек (1-«дүйсенбі», 2-«сейсенбі»,...).

5.2. k бүтін саны берілген. Берілген санға сай келетін бағаның атауын шығару керек. (1-«нашар», 2-«қанағаттанғысыз», 3-«қанағаттанарлық», 4-«жақсы», 5-«өте жақсы»). Егер k -ның мәні 1-5 аралығында жатпаса, «қате» сөзі шығарылсын.

5.3. 1-12 аралығындағы бүтін сан – ай нөмірі берілген (1-қаңтар, 2-ақпан, т.с.с.). Кібісе емес жыл үшін ендірілген нөмірлі айдағы күн санын анықтау керек.

5.4. 1-12 аралығындағы бүтін сан – ай нөмірі берілген (1-қаңтар, 2-ақпан, т.с.с.). Сәйкес жыл мезгілін анықтау керек («қыс», «көктем», «жаз», «күз»).

5.5. Сандарға қолданылатын арифметикалық амалдар былайша нөмірленген: 1-қосу, 2-азайту, 3-көбейту, 4-бөлу. Амал нөмірі n (1-4 аралығындағы сан) және a,b (b – нөлден өзге сан) нақты сандары берілген. Сандарға көрсетілген амалды орындап, нәтижені шығару керек.

5.6. Ұзындық өлшемдері былайша нөмірленген: 1-дециметр, 2-километр, 3-метр, 4-миллиметр, 5-сантиметр. Ұзындық бірлігінің нөмірі (1-5 аралығындағы бүтін сан) және кесіндінің осы бірліктегі ұзындығы (нақты сан) берілген. Кесінді ұзындығын метрмен табу керек.

5.7. Салмақ өлшемдері былайша нөмірленген: 1-килограмм, 2-миллиграмм, 3-грамм, 4-тонна, 5-центнер. Салмақ бірлігінің нөмірі (1-5 аралығындағы нақты сан) және дене ауырлығының осы бірліктегі салмағы (нақты сан) берілген. Дене салмағын килограммен табу керек.

5.8. Кібісе емес жылдағы күн мен айды анықтайтын d және m айнымалылары берілген. Берілген күннен алдыңғы күн (d) мен айды (m) шығару керек.

5.9. Кібісе емес жылдағы күнді және айды анықтайтын d және m айнымалылары берілген. Берілген күннен кейінгі күн (d) мен айды (m) шығару керек.

5.10. Робот төрт бағытта қозғала алады (Ш-шығыс, Б-батыс, О-оңтүстік, С-солтүстік) және үш цифрлық нұсқауды қабылдай алады: 0 – қозғалысты жалғастыру, 1 – солға бұрылу, -1 – оңға бұрылу. Роботтың бастапқы қозғалыс бағыты t мен n бүтін саны (цифрлық нұсқау) берілген. Берілген нұсқауды орындаған соң роботтың бағытын шығару керек.

5.11. Локатор жер шары тараптарының біріне бағытталған (Ш-шығыс, Б-батыс, О-оңтүстік, С-солтүстік) және үш цифрлық бұрылу нұсқауларын қабылдай алады: 1 – солға бұрылу, -1 – оңға бұрылу, 2 – 180°-қа бұрылу. Локатордың бастапқы бағыты d және n₁,n₂ – цифрлық нұсқаулары берілген. Нұсқаулар орындалған соң локатордың бағыты қалай өзгереді?

5.12. Шеңбер элементтері былай нөмірленген: 1 – радиус (R), 2 – диаметр (d=2×R), 3 – ұзындық (L=2×p×R), 4 – дөңгелек ауданы (S=p×R²). Осы элементтердің бірінің нөмірі мен мәні берілген. Барлық басқа элементтердің мәні табылып, көрсетілген тәртіп бойынша шығарылуы керек.

5.13. Тең бүйірлі тік бұрышты үшбұрыш элементтері былайша нөмірленген: 1 – катеті (а), 2 –гипотенузасы (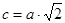), 3 – гипотенузаға түсірілген биіктігі (h=c/2), 4 – ауданы (S=с×h/2). Осы элементтердің бірінің нөмірі мен мәні берілген. Үшбұрыштың қалған элементтерінің мәні табылып, көрсетілген тәртіп бойынша шығарылуы керек.

5.14. Тең қабырғалы үшбұрыш элементтері былайша нөмірленген: 1 – қабырғасы (а), 2 – іштей сызылған шеңбер радиусы (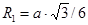), 3 – сырттай сызылған шеңбер радиусы (R₂=2×R₁), 4 – ауданы (). Осы элементтердің бірінің нөмірі мен мәні берілген. Үшбұрыштың қалған элементтердің мәні табылып, көрсетілген тәртіп бойынша шығарылуы керек.

5.15. Ойын карталарының суреттері былай нөмірленген: 1 – «кірпіш (қиық)», 2 – «қарға», 3 – «жүрек (түйе)», 4 – «шыбын». Нөмірі 10-нан жоғары карталар былай дәрежеленген: 11 – «валет», 12 – «дама», 13 – «король», 14 – «тұз». Екі бүтін сан берілген: n – карта дәрежесі (6 ≤ n ≤ 14) және m – карта суреттері (1 ≤ m ≤ 4). Осы мәліметтер бойынша сәйкес картаның атауын шығару керек, мысалы, «валет шыбын», «тоғыз кірпіш», «тұз жүрек», т.с.с.

5.16. Жасты жылдармен анықтайтын 18-59 аралығындағы n бүтін саны берілген. Адамды туылған күнімен құттықтау мәтіні құрастырылып шығарылсын. «Туылған күніңіз құтты болсын! …» мәтініндегі көп нүктенің орнына егер адамның жасы 0-мен аяқталса – «n – мәртебелі жас!» сөзі, 5-пен аяқталса – «n – керемет жас!» сөзі, 24,36,48 болса – «n – мүшел жас!» сөзі тіркеледі, ал қалғандары үшін ешқандай мәтін тіркелмейді.

5.17. k – екі таңбалы бүтін саны берілген. Оның атауын сөзбен жазу керек. Мысалы, 24 – «жиырма төрт», 56 – «елу алты», 80 – «сексен», т.с.с.

5.18. k – үш таңбалы бүтін саны берілген. Оның атауын сөзбен жазу керек. Мысалы, 274 – «екі жүз жетпіс төрт», 756 – «жеті жүз елу алты», 809 – «сегіз жүз тоғыз», т.с.с.

5.19. Шығыс күнтізбесінде 60 жылдық цикл кеңінен қолданылады. Өз кезегінде бұл цикл 12 жылдық ішкі циклдарға бөлінеді және олар түстермен ажыратылады: жасыл, қызыл, сары, ақ және қара. Әрбір ішкі циклдағы жылдар жануарлар атауымен аталады: тышқан, сиыр, барыс, қоян, ұлу, жылан, жылқы, қой, мешін, тауық, ит және доңыз. Енгізілген жыл нөмірі бойынша оның атауын шығару керек. Мысалы, 1984 – «жасыл тышқан жылы» (жаңа циклдың басы), 2014 – «сары жылқы жылы», т.с.с.

5.20. Күн мен айды анықтайтын d және m бүтін сандары берілген. Осы күнге сәйкес келетін Зодиак таңбасын шығару керек: «Суқұйғыш» (20.1-18.2), «Балықтар» (19.2-20.3), «Тоқты» (21.3-19.4), «Торпақ» (20.4-20.5), «Егіздер» (21.5-21.6), «Шаяндар» (22.6-22.7), «Арыстан» (23.7-22.8), «Бикеш» (23.8-22.9), «Таразы» (23.9-22.10), «Сарышаян» (23.10-22.11), «Мергендер» (23.11-21.12), «Тауешкі» (22.12-19.1).

6. Параметрлі қайталау (FOR циклы)

6.1. k және n бүтін сандары берілген (n>0). k санын n рет шығару керек.

6.2. a және b бүтін сандары берілген (a<b). Олардың арасындағы барлық бүтін сандарды a және b сандарының өздерін қоса өсу тәртібімен шығару керек және олардың нешеу екенін анықтау керек.

6.3. a және b бүтін сандары берілген (a<b). Олардың арасындағы барлық бүтін сандарды a және b сандарының өздерін қоса кему тәртібімен шығару керек және олардың нешеу екенін анықтау керек.

6.4. 1 кг кәмпит бағасы болатын n нақты саны берілген. 1, 2, …, 10 кг кәмпиттің құнын есептеу керек.

6.5. 1 кг кәмпит бағасы болатын n нақты саны берілген. 0.1, 0.2, …, 1.0 кг кәмпиттің құнын есептеу керек.

6.6. 1 кг кәмпит бағасы болатын n нақты саны берілген. 1.2, 1.4, …, 2.0 кг кәмпиттің құнын есептеу керек.

6.7. a және b бүтін сандары берілген (a<b). a және b сандарымен бірге олардың арасындағы барлық бүтін сандардың қосындысын табу керек.

6.8. a және b бүтін сандары берілген (a<b). a және b сандарымен бірге олардың арасындағы барлық бүтін сандардың көбейтіндісін табу керек.

6.9. a және b бүтін сандары берілген (a<b). a және b сандарымен бірге олардың арасындағы барлық бүтін сандардың квадраттарының қосындысын табу керек.

6.10. Оң n бүтін саны берілген. Келесі қосындыны есептеу керек: 1+1/2+1/3+…+1/n.

6.11. Оң n бүтін саны берілген. Келесі қосындыны есептеу керек: n²+(n+1)²+(n+2)²+…+(2×n)² (бүтін сан).

6.12. Оң n бүтін саны берілген. Келесі көбейтіндіні есептеу керек: 1.1×1.2×1.3×… (көбейткіштер саны n).

6.13. Оң n бүтін саны берілген. Келесі өрнектің мәнін табу керек:

1.1 – 1.2 + 1.3 – …

(қосылғыштар саны n, таңбалар кезектеседі). Тармақталу операторын

қолдануға болмайды.

6.14. Оң n бүтін саны берілген. Берілген санның квадраты келесі формуланы пайдаланып шығарылсын:

n² = 1 + 3 +5 + … +(2×n-1)

Қосындыға әрбір қосылғыш қосылған кезде қосындының соңғы мәні

шығарылсын. Бұл – 1-ден n-ге дейінгі барлық бүтін сандардың

квадраттарын береді.

6.15. Нақты а және оң бүтін n саны берілген. а -ның n дәрежесін есептеу керек: аⁿ = a× a× a× … (а саны өзіне-өзі n рет көбейтіледі).

6.16. Нақты а және оң бүтін n саны берілген. Бір ғана циклды пайдаланып, а -ның 1-ден n- ге дейінгі барлық бүтін дәрежелерін есептеу керек.

6.17. Нақты а және оң бүтін n саны берілген. Бір ғана циклды пайдаланып, келесі қосындының мәнін есептеу керек:

1 + a + a² + a³ + …+ aⁿ.

6.18. Нақты а және оң бүтін n саны берілген. Бір ғана циклды пайдаланып, келесі өрнектің мәнін есептеу керек:

1 – a + a² – a³ + …+(-1)ⁿaⁿ.

Тармақталу операторын қолдануға болмайды.

6.19. Оң бүтін n саны берілген. Келесі көбейтіндіні есептеу керек:

n!=1×2×…× n (n-факториал).

Бүтін санды «тасқынды» болдырмау үшін көбейтіндіні нақты айнымалы

арқылы орындап, нәтижені нақты сан ретінде шығару керек.

6.20. Оң бүтін n саны берілген. Бір ғана циклды пайдаланып, келесі қосындының мәнін есептеу керек:

1! + 2! + 3! + …+ n!

(n! – n-факториал өрнегі 1-ден n -ге дейінгі бүтін сандардың көбейтінді-

сін береді, яғни n!=1×2×…× n). Бүтін санды «тасқынды» болдырмау үшін

көбейтіндіні нақты айнымалы арқылы орындап, нәтижені нақты сан

ретінде шығару керек.

6.21. Оң бүтін n саны берілген. Бір ғана циклды пайдаланып, келесі қосындының мәнін есептеу керек:

1 + 1/(1!) + 1/(2!) + 1/(3!) + …+ 1/(n!)

(n!=1×2×…× n). Алынған нәтиже е = exp(1) тұрақтысының жуық мәні

болып табылады.

6.22. Нақты х саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

1 + х/(1!) + х²/(2!) + х³/(3!) + …+ xⁿ/(n!)

(n!=1×2×…× n). Алынған нәтиже exp(x) функциясының x нүктесіндегі

жуық мәні болып табылады.

6.23. Нақты х саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

х – х³/(3!) + х⁵/(5!) – …+ (-1)ⁿ× x^{2× n+1}/((2× n+1)!)

(n!=1×2×…× n). Алынған нәтиже sin(x) функциясының x нүктесіндегі

жуық мәні болып табылады.

6.24. Нақты х саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

1 – х²/(2!) + х⁴/(4!) – …+ (-1)ⁿ× x^{2× n}/((2× n)!)

(n!=1×2×…× n). Алынған нәтиже cos(x) функциясының x нүктесіндегі

жуық мәні болып табылады.

6.25. Нақты х (|x|<1) саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

x – х²/2 + х³/3 – …+ (-1)^n-1× x ⁿ/ n

Алынған нәтиже ln функциясының 1+x нүктесіндегі жуық мәні болып

табылады.

6.26. Нақты х (|x|<1) саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

x – х³/3 + х⁵/5 – …+ (-1)ⁿ× x ^{2× n+1}/(2× n+1)

Алынған нәтиже arctg функциясының x нүктесіндегі жуық мәні болып

табылады.

6.27. Нақты х (|x|<1) саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

x +1× х³/(2× 3) + 1× 3× х⁵/(2× 4× 5) +…

+ 1× 3×…× (2×n –1)× x ^{2× n+1}/(2× 4×…(2×n)× (2× n+1)

Алынған нәтиже arcsin функциясының x нүктесіндегі жуық мәні болып

табылады.

6.28. Нақты х (|x|<1) саны мен оң бүтін n саны берілген. Келесі өрнектің мәнін табу керек:

1 + х/2 – 1× х²/(2× 4) + 1× 3× х³/(2× 4× 6) – …

+ (-1)^n-1× 1× 3×…× (2×n –3)× x ⁿ/(2× 4×…(2× n)).

Алынған нәтиже функциясының жуық мәні болып табылады.

6.29. Оң бүтін n саны және сан осіндегі a,b (a<b) екі нақты саны берілген. [a,b] кесіндісі n тең бөлікке бөлінген. Әрбір кесіндінің ұзындығы (h) мен [a,b] кесіндісін бөлу нүктелерін құрайтын келесі тізбекті шығару керек:

a, a+h, a+2× h, a+3× h, … b.

6.30. Оң бүтін n саны және сан осіндегі a,b (a<b) екі нақты саны берілген. [a,b] кесіндісі n тең бөлікке бөлінген. Әрбір кесіндінің ұзындығы (h) мен [a,b] кесіндісін бөлу нүктелеріндегі f(x)=1-sin(x) функциясының мәндерін шығару керек:

f(a), f(a+h), f(a+2× h), f(a+3× h), … f(b).

6.31. Оң бүтін n саны берілген. a_k нақты сандар тізбегі былай анықталады:

a₀=2, a_k=2+1/ a_k-1, k=1,2,….

a₁, a₂,…, a_n элементтерін шығару керек.

6.32. Оң бүтін n саны берілген. a_k нақты сандар тізбегі былай анықталады:

a₀=1, a_k= (a_k-1+1)/k, k=1,2,….

a₁, a₂,…, a_n элементтерін шығару керек.

6.33. Бүтін n (n>1) саны берілген. f_k бүтін сандар тізбегі (Фибоначчи сандары) былай анықталады:

f₁=1, f₂=1, f_k= f_k-2+ f_k-1, k=3,4,….

f₁, f₂,…, f_n элементтерін шығару керек.

6.34. Бүтін n (n>1) саны берілген. a_k нақты сандар тізбегі былай анықталады:

a₁=1, a₂=2, a_k= (a_k-2+2× a_k-1)/3, k=3,4,….

a₁, a₂,…, a_n элементтерін шығару керек.

6.35. Бүтін n (n>2) саны берілген. a_k бүтін сандар тізбегі былай анықталады:

a₁=1, a₂=2, a₃=3, a_k= a_k-1+a_k-2 – 2× a_k-3, k=4,5,….

a₁, a₂,…, a_n элементтерін шығару керек.

Не нашли, что искали? Воспользуйтесь поиском: