
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Несобственные интегралы
Рассмотрим  . Функция
. Функция  определена на конечном промежутке
определена на конечном промежутке  и ограничена на нем. Если нарушается хотя бы одно из двух требований, то мы имеем дело с несобственным интегралом.
и ограничена на нем. Если нарушается хотя бы одно из двух требований, то мы имеем дело с несобственным интегралом.
1. Пусть нарушается требование конечности чисел a и (или) b. При этом возможны случаи:
1) пусть  определена на
определена на  и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке  , где
, где  (рис. 3).
(рис. 3).
Несобственным интегралом первого рода называется  и обозначается
и обозначается  , то есть
, то есть  (1).
(1).
Если предел в правой части равенства (1) существует и конечен, то несобственный интеграл называется сходящимся и его значение равно пределу правой части. В противном случае несобственный интеграл называется расходящимся.
| Рис. 3 |

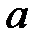


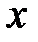







| Рис. 4 |
2) пусть  определена на
определена на  и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке  ,
,  (рис. 4).
(рис. 4).
Несобственный интеграл первого рода в этом случае определяется по формуле  (2).
(2).
3) пусть  определена на
определена на  и интегрируема на каждом конечном отрезке этого интервала, тогда
и интегрируема на каждом конечном отрезке этого интервала, тогда  (3), причем несобственный интеграл в левой части называется сходящимся, если сходятся оба интеграла в правой части равенства (3). Если хотя бы один из них расходится, то расходится интеграл в левой части.
(3), причем несобственный интеграл в левой части называется сходящимся, если сходятся оба интеграла в правой части равенства (3). Если хотя бы один из них расходится, то расходится интеграл в левой части.
Замечание. Если  первообразная функции
первообразная функции  на
на  , тогда справедлива обобщенная формула Ньютона-Лейбница
, тогда справедлива обобщенная формула Ньютона-Лейбница 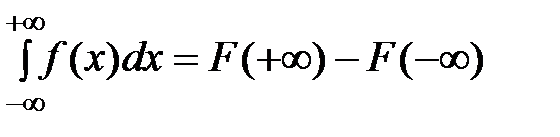 , где
, где  ,
,  .
.
Пример. 
2. Пусть нарушается требование ограниченности функции  .
.
1) Пусть функция  непрерывна на
непрерывна на  и
и  , тогда
, тогда  (4).
(4).
2) Если  непрерывна на
непрерывна на  и
и  , тогда
, тогда  (5).
(5).




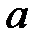


| Рис. 5 |
3) Если  непрерывна на
непрерывна на  и
и  (рис. 5), тогда
(рис. 5), тогда
 (6).
(6).
Интеграл в левой части равенства (6) называется сходящимся, если сходятся оба интеграла в правой части этой формулы; и расходящимся, если расходится хотя бы один из интегралов в правой части этой формулы.
Не нашли, что искали? Воспользуйтесь поиском: