
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задачи
Пример 1. Написать три первых члена степенного ряда  , найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
, найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
Решение.
1) Запишем три первых члена степенного ряда:
при n=0  ,
,
при n=1  ,
,
при n=2  .
.
2) Найдем радиус сходимости степенного ряда по формуле (3). Для этого запишем коэффициенты рассматриваемого ряда  и
и  . Тогда
. Тогда


следовательно, промежуток (-2;2) является интервалом сходимости ряда.
3) Исследуем поведение ряда на концах интервала сходимости в точках x=-2 и x=2.
При x=-2 получим знакочередующийся ряд

Модуль общего члена данного ряда имеет вид  Ряд расходится, так как не выполняется одно из условий признака Лейбница
Ряд расходится, так как не выполняется одно из условий признака Лейбница
,
то есть общий член ряда не стремится к нулю.
При x=2 получим ряд

Этот ряд расходится, так как не выполнен необходимый признак сходимости:
 .
.
Таким образом, на обоих концах интервала сходимости ряд расходится.
Ответ: интервал сходимости степенного ряда (-2;2).
Пример 2. Найти интервал сходимости ряда  и исследовать его сходимость на концах этого интервала.
и исследовать его сходимость на концах этого интервала.
Решение.
1) Найдем радиус сходимости степенного ряда по формуле (3). Для этого запишем коэффициенты рассматриваемого ряда 
 , тогда
, тогда

 следовательно, промежуток
следовательно, промежуток  является интервалом сходимости ряда.
является интервалом сходимости ряда.
2) Исследуем поведение ряда на концах интервала сходимости в точках  и
и .
При  получим знакочередующийся ряд
получим знакочередующийся ряд
 .
.
Данный ряд сходится по признаку Лейбница, так как:
а) абсолютные величины членов ряда монотонно убывают  ,
,
то есть 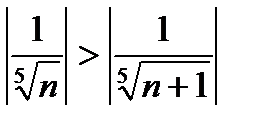 ;
;
б) предел модуля общего члена ряда равен нулю при 

При  получим ряд
получим ряд 
Полученный ряд расходится как обобщенный гармонический ряд с показателем  .
.
Ответ: ряд сходится при  .
.
Пример 3. Найти интервал сходимости ряда  и исследовать его сходимость на концах этого интервала.
и исследовать его сходимость на концах этого интервала.
Решение.
1) Найдем радиус сходимости степенного ряда по формуле (4). Для этого запишем коэффициент рассматриваемого ряда  , тогда
, тогда

следовательно, промежуток  является интервалом сходимости ряда.
является интервалом сходимости ряда.
2) Исследуем поведение ряда на концах интервала сходимости в точках  и
и 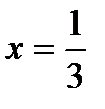 .
.
При  получим знакочередующийся ряд
получим знакочередующийся ряд

Ряд расходится, так как не выполняется одно из условий признака Лейбница – абсолютные величины членов ряда не убывают.
При  получим ряд
получим ряд
 .
.
Полученный ряд расходится, так как не выполнен необходимый признак сходимости:
 .
.
Замечание. При вычислении предела была использована формула

Ответ: ряд сходится при  .
.
Пример 4. Найти интервал сходимости ряда  и исследовать его сходимость на концах этого интервала.
и исследовать его сходимость на концах этого интервала.
Решение.
1) Применим признак Даламбера. Учитывая, что  ,
,
 , найдем предел
, найдем предел

 .
.
Для сходимости ряда полученный предел должен быть меньше единицы, то есть  или -3<x<1.
или -3<x<1.
Следовательно, промежуток (-3;1) является интервалом сходимости ряда.
2) Исследуем поведение ряда на концах интервала сходимости в точках  и
и  .
.
При 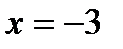 получим знакочередующийся ряд
получим знакочередующийся ряд
 .
.
Данный ряд сходится по признаку Лейбница, так как:
а) абсолютные величины членов ряда монотонно убывают 
то есть 
б) предел модуля общего члена ряда равен нулю при 

При  получим гармонический ряд
получим гармонический ряд
 ,
,
который, как известно, расходится.
Ответ: ряд сходится при  .
.
ЗАДАНИЕ 9
В задачах 9.1-9.20 вычислить с точностью до 0,001 определенный интеграл  , используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда.
, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда.
Данные к заданию представлены в Приложении 9.
Не нашли, что искали? Воспользуйтесь поиском: