Вопрос 4. Предел числовой последовательности. Предел функции.

Предел числовой последовательности

Назовем числовой последовательностью ряд значений функции целочисленного переменного. Если изображать элементы бесконечной последовательности точками числовой оси, то может оказаться, что все члены последовательности начиная с некоторого номера окажутся внутри интервала 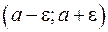, окружающего некоторую точку 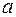. Если величина 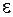с увеличением номера 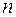убывает и стремится к нулю, то число 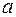называют пределом последовательности 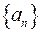и пишут . 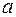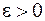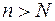Второе определение предела: число называется пределом последовательности , если для любого, сколь угодно малого найдется номер такой, что при номере будет

Понятие предела является удобным инструментом исследования бесконечных процессов. Действительно, если бесконечная последовательность имеет пределом число 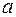, то с известной точностью 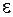она может быть приближенно заменена конечной последовательностью .

Предел функции непрерывного аргумента.

Число 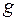называют пределом функции при стремящимся к бесконечности и пишут 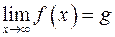, если для любого сколь угодно малого 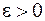найдется положительное число , зависящее от 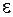, сколь угодно большое такое, что при 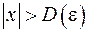будет .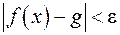

Число 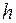называют пределом функции при стремящемся к 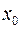и пишут 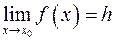, если для любого сколь угодно малого 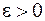существует число 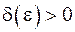такое, что 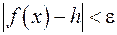при .

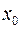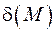Функция при стремящемся к имеет бесконечный предел, если каково бы ни было сколь угодно большим положительное число , существует число такое, что при 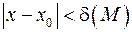будет .

Не нашли, что искали? Воспользуйтесь поиском: