ТЕМА. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ.

Вопрос 8. Производная функции. Геометрический смысл производной. Основные правила дифференцирования. Таблица производных.

Таблица производных основных элементарных функций.

Производной функции 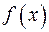в точке называют следующий предел 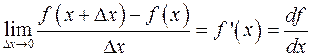, где и – условные обозначения производной. Операция нахождения производной получила название дифференцирования.

Понятие производной встречается при решении многих математических и физических задач и является важной характеристикой функции.

Геометрический смысл производной: производная равна тангенсу угла наклона касательной к оси 0Х.

Основные правила дифференцирования. Таблица производных.

1. , с – const.

2.

3.

4.

5.

Таблица производных основных элементарных функций.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. .

Вопрос 9. Производная сложной функции. Производная обратной функции. Производные высших порядков. Производная неявно заданной функции. Логарифмическое дифференцирование, дифференцирование функций, заданных параметрически.

Если , а переменная в свою очередь является функцией , то по отношению к переменной функцию называют сложной. Примеры сложных функций: .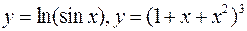

Правило дифференцирования сложной функции: .

Для монотонной функции существует обратная функция . Если функция дифференцируема, то производная обратной функции существует и находится по формуле .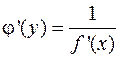

Производную функции в свою очередь можно дифференцировать. В результате получим производную второго порядка . Дифференцируя далее, будем находить производные третьего , четвертого и вообще n-го порядка.

При неявном задании функция определяется как возможное решение уравнения . Производную такой функции можно найти, не прибегая к явному выражению функции.

Пример 8.

Найти производную функции в точке А.

, .

Найдем производную функции , заданную неявно уравнением кривой. С этой целью продифференцируем обе части уравнения, считая аргументом, а – функцией от

.

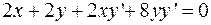Отсюда .

В некоторых случаях непосредственное дифференцирование функции является очень громоздким. Тогда может оказаться полезным предварительно ее прологарифмировать.

Пример 9.

,

,

.

Отсюда, .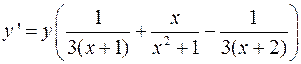

Пример 10.

,

,

.

При параметрическом задании переменные и задаются как функции параметра : , . При этом в неявной форме устанавливается зависимость ,которую можно найти, если из первого параметрического уравнения выразим и подставим во второе: .

Правило дифференцирования параметрически заданных функций:

.

Пример.

Не нашли, что искали? Воспользуйтесь поиском: