
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вопрос 6. Эквивалентные бесконечно малые. Применение эквивалентности при вычислении пределов функций
Функция называется бесконечно малой при  (или
(или 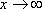 ), если
), если  (или).
(или). 
Так как  , то при
, то при 
 - бесконечно малая. Однако cos(x) не является бесконечно малой при
- бесконечно малая. Однако cos(x) не является бесконечно малой при  , так как
, так как  . Одна и та же функция может быть бесконечно малой или не быть в зависимости от предельного значения x0. Есть функции, например x2+1, которые не могут быть бесконечно малыми ни при каких условиях.
. Одна и та же функция может быть бесконечно малой или не быть в зависимости от предельного значения x0. Есть функции, например x2+1, которые не могут быть бесконечно малыми ни при каких условиях.
Две бесконечно малые называются эквивалентными, если предел их отношения равен 1.

При вычислении пределов часто применяется следующая Теорема. Предел отношения двух бесконечно малых (неопределенность) равен пределу отношения двух других бесконечно малых, эквивалентных данным, т.е. 
Отметим также: если  , то
, то  .
.
Основные формулы эквивалентности бесконечно малых.
Первая группа формул эквивалентности бесконечно малых.
При 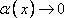

 . (1)
. (1)
Вторая группа формул эквивалентности бесконечно малых.

 (2)
(2)
Третья группа формул эквивалентности бесконечно малых.

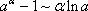



Четвертая группа формул эквивалентности бесконечно малых.


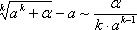



Не нашли, что искали? Воспользуйтесь поиском: