Вопрос 11. Теоремы о среднем. Правило Лопиталя-Бернулли.

Пусть функция 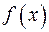непрерывна в интервале 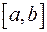и дифференцируема в интервале . Тогда имеют место теоремы:

1) Теорема Ролля: если , то непременно существует точка , в которой .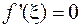

2) Теорема Лагранжа: На интервале непременно существует точка , в которой .

3) Теорема о возрастании и убывании функции: Если на интервале , то на этом интервале функция 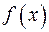монотонно возрастает; при 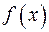монотонно убывает.

4) Теорема Коши: Пусть функция 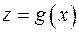непрерывна и монотонна на интервале 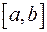и дифференцируема на интервале , тогда имеет место формула

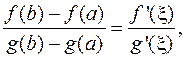где .

Правило Лопиталя-Бернулли.

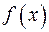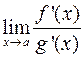Пусть . Если функции и дифференцируемы в окрестности точки , и существует конечный или бесконечный предел , то .

Правило Лопиталя-Бернули справедливо также для случая, когда .

Пример 11.

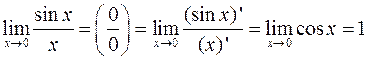
Не нашли, что искали? Воспользуйтесь поиском: