Признаки возрастания функции.

Если дифференцируемая функция y=f(x) в интервале (a,b) возрастает, то её производная в этом интервале неотрицательна, т.е.

Если непрерывная на отрезке [a,b] и дифференцируемая внутри него функция y=f(x) имеет положительную производную, то f- возрастает на этом отрезке:

Признаки убывания функция y=f(x) на отрезке [a,b] формулируются аналогично и связываются с отрицательностью производной .

Экстремумом функции называют ее минимальное или максимальное значение.

Определение минимума (максимума): непрерывная функция 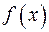имеет в точке минимум или максимум, если в достаточно малой окрестности этой точки (слева и справа от нее) все значения функции больше минимального , и все значения функции меньше в случае, когда – точка минимума.

На графике точка экстремума соответствует впадине (минимум) или выступу (максимум). Понятие экстремума относится только к некоторой ограниченной области. Вне ее функция может принимать значения больше максимального или меньше минимального. В связи с этим наряду с экстремумом вводится понятие наибольшего и наименьшего значения функции, как самого большого и самого малого, которые принимает функция на некотором интервале. Наибольшее и наименьшее значение функции выбираются среди ее экстремальных значений и значений на границах интервала.

В точке экстремума касательная к графику функции горизонтальна. Отсюда следует необходимый признак экстремума: если в точке экстремума производная функции существует, то она равна нулю. Однако равенство нулю производной не гарантирует наличие экстремума (необходимый признак не является достаточным). Например, производная функции при обращается в нуль, но экстремума в этой точке нет.

Рисунок 11.

Полностью вопрос об экстремумах решается с помощью необходимого и достаточного признака существования экстремума: функция имеет в точке экстремум, если производная меняет знак при переходе через эту точку; экстремум является минимумом при изменении знака производной с (-) на (+) и максимумом при изменении знака с (+) на (-).

Пример 14.

1. Исследовать на экстремум функцию

Дифференцируем функцию и отыскиваем нули ее производной

,

,

,

,

.

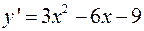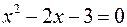Исследуем знак производной:

на интервале будет ,

-

-

Отсюда при 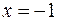функция имеет максимум ; при - минимум .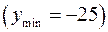

Задачи на отыскание наименьших и наибольших значений.

Рассмотренный метод отыскания экстремальных значений функции широко применяется при решении прикладных задач, в которых требуется отыскать наибольшее или наименьшее значение какого-нибудь параметра.

Не нашли, что искали? Воспользуйтесь поиском: