Вопрос 16. Приложения производной к исследованию функций и построению графиков. Асимптоты графика функции.

Асимптотой называют прямую, к которой неограниченно близко приближается график функции. Асимптоты характеризуют поведение функции при больших значениях аргумента или функции и удобны при построении графиков.

По методу нахождения различают вертикальные и наклонные асимптоты.

Вертикальную асимптоту функция 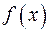имеет в том случае, если у нее есть точка бесконечного разрыва . Уравнение вертикальной асимптоты будет .

Наклонная асимптота имеет уравнение .

и .

Пример 16.

Найти асимптоты графика функции

В точке функция имеет точку бесконечного разрыва, поэтому уравнение вертикальной асимптоты будет . Определим теперь коэффициенты уравнения наклонной асимптоты:

.

Таким образом, наклонная асимптота имеет уравнение .

Не нашли, что искали? Воспользуйтесь поиском: