
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вопрос 15. Приложения производной к исследованию функций и построению графиков. Выпуклость, вогнутость, точки перегиба.
Вогнутость кривой
Кривая называется вогнутой вверх в точке  , если она лежит выше своей касательной, и вогнутой вниз - если ниже. Направление вогнутости кривой аналитически определяется по закону второй производной посредством признака вогнутости: если на интервале
, если она лежит выше своей касательной, и вогнутой вниз - если ниже. Направление вогнутости кривой аналитически определяется по закону второй производной посредством признака вогнутости: если на интервале 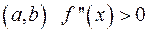 , то при этом интервале кривая
, то при этом интервале кривая  вогнута вверх; при
вогнута вверх; при  кривая вогнута вниз.
кривая вогнута вниз.
Точка кривой, в которой происходит изменение направления вогнутости, называют точкой перегиба. Признаком существования точки перегиба является изменение знака второй производной при переходе через эту точку. Точки перегиба отыскиваются среди нулей и точек разрыва  .
.
По направлению вогнутости кривой можно определить характер экстремума функции: если  , то в точке
, то в точке  функция
функция 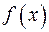 имеет минимум, если
имеет минимум, если  , и максимум, если
, и максимум, если  .
.
Данный признак является следствием того, что в точке максимума график функции вогнут вниз, а в точке минимума вверх.
Пример 15.
Исследовать на экстремум функцию  .
.
Эта функция имеет производную 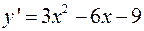 , которая обращается в нуль в точках
, которая обращается в нуль в точках  и
и  . Вторая производная функции равна
. Вторая производная функции равна  . При этом
. При этом 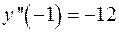 и
и  . Согласно вышеуказанному признаку при
. Согласно вышеуказанному признаку при 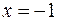 функция имеет максимум, а при
функция имеет максимум, а при  - минимум.
- минимум.
Не нашли, что искали? Воспользуйтесь поиском: