Вопрос 17. Приложение производной к исследованию функций и построению графиков. Общая схема исследования.

Общая схема исследования.

1. Область определения. Точки разрыва.

2. Четность, нечетность.

3. Периодичность.

4. Интервалы знакопостоянства.

5. Интервалы возрастания, убывания, экстремумы.

6. Интервалы выпуклости, вогнутости, точки перегиба.

7. Асимптоты.

8. Дополнительные точки.

Пример 17.

Исследовать функцию и построить ее график.

1. Устанавливаем область определения функции, находим точки разрыва, исследуем поведении функции в окрестности этих точек, а также на границах области определения.

Заданная функция определена на всей действительной оси за исключением точек 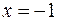и , в которых она имеет разрыв. При приближении к этим точкам функция неограниченно возрастает. Поэтому прямые 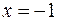и являются вертикальными асимптотами функции. При неограниченном возрастании или убывании функция стремится к .

2. Исследуем функцию на четность и нечетность, определяем интервалы знакопостоянства функции.

Функция четна, так как 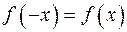, ее график симметричен относительно оси ординат.

3. Функция не имеет периода.

4. Для исследования знака функции разбиваем область ее определения на интервалы точками, в которых она обращается в нуль или имеет разрыв, и определяем знак функции в каждом из этих интервалов. На интервалах и функция отрицательна; на интервале - положительна. При переходе через нуль функции () функция знака не меняет, следовательно, прямая касается графика функции в точке .

5. Исследовав первую производную, определяем интервалы возрастания и убывания функции, находим точки экстремума.

Производная функции равна

.

Функция изменяет знак только при переходе через точки, в которых она обращается в нуль или имеет разрыв. Поэтому знак производной определяем в каждом из следующих интервалов: и . Находим: в интервалах и - ; в интервалах и - . Следовательно, в двух первых интервалах функция убывает, а в последних - возрастает. При производная функции обращается в нуль, и при переходе через эту точку производная меняет знак с (-) на (+). Поэтому в точке функция имеет минимум - .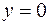

6. Изучив вторую производную, находим интервалы вогнутости вверх и вниз графика функции, определяем точки перегиба.

Вторая производная функции равна

.

Она отрицательна при 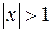и положительна при 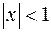. Поэтому на интервалах и график функции вогнут вниз, а на интервале - вверх. Вторая производная нигде не обращается в нуль (функция, стоящая в числителе, всегда положительна), и поэтому график не имеет точек перегиба.

7. Находим наклонные и горизонтальные асимптоты функции.

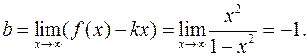
Функция имеет:

горизонтальную асимптоту y = -1;

вертикальные асимптоты x = -1; x = 1.

Проведенное исследование устанавливает общий характер изменения функции и позволяет построить ее график. Построение графика рекомендуется начать с проведения асимптот и отметки точек, в которых функция и ее две производные или обращаются в нуль, или имеют точки разрыва. График исследованной функции изображен на рис.12.

Рисунок 12.

Не нашли, что искали? Воспользуйтесь поиском: