Q – сила полезного сопротивления. 2 страница

R₄₃ + G₄ + U₄ + R₄₅ = 0.

В этом уравнении одно неизвестное - R₄₅. Для его определения можно не строить отдельный векторный многоугольник, а выделить в многоугольнике диады вектора, входящие в это уравнение, и построить замыкающий вектор.

Перейдем к исследованию диады 2-3. Изобразим ее отдельно, заменив действие отброшенных звеньев реакциями. Расчет диады 2-3 выполняется точно также, как и диады 4-5.

Кривошип находится под действием уравновешивающей силы P_ур, реакции со стороны 2-го звена R₁₂, реакции со стороны стойки R₁₀. Поскольку P_ур и R₁₂ приложены в одной точке, они дают равнодействующую, которая уравновешивается реакцией R₁₀. Отсюда следует, что R₁₀ направлена по звену. Уравнение равновесия кривошипа

P _ур + R₁₀ + R₁₂ = 0.

Из треугольника сил находятся реакции R₁₀ и P_ур.

3.8. Метод рычага Жуковского

Метод рычага Жуковского представляет геометрическую интерпретацию принципа возможных перемещений. Он применяется для плоских механизмов и позволяет определить уравновешивающую силу без предварительного определения реакций в кинематических парах. Принцип возможных перемещений (принцип Даламбера – Лагранжа) находит широкое применение в механике. Он формулируется следующим образом: работа всех активных сил и сил инерции на возможном перемещении системы равна нулю. Этот принцип эквивалентен закону сохранения энергии для механических систем. Он записывается в виде

ΣF_K • δ r_K = 0, (3.3)

где в левой части стоит сумма скалярных произведений векторов сил F_K на векторы возможных перемещений точек приложения этих сил δr_K.

Разделим выражение (3.3) на δt:

ΣF_K δr_K / δt = ΣF_k • V_k = Σ|F_K | | V_K | cos (F_k • V_k) = 0.

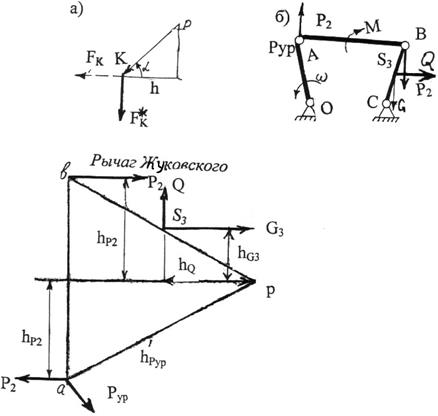
Рис 3.8. Метод рычага Жуковского

Рассмотрим элемент плана скоростей, на котором изображена скорость точки К. Приложим к точке К вектор F_K^*, изображающий силу F_K,, повернутую на 90˚ относительно ее истинного направления. Из построения на рис. 3.8а следует:

h = pk cos α = V_K cos α / k_v= V_K cos (F_K, V_K) / k_v. (3.4)

Если рассматривать отрезок pk как рычаг, закрепленный в точке р, то сила F_K^* создает момент:

M_K = F_K^* h = |F_K^* | |V_K | cos (F_K V_K) / k_v. (3.5)

Из сравнения выражений (3.4) и (3.5) следует, что с точностью до множителя k_v

ΣF_K δr_k / δt = ΣM_K = 0.

Полученный результат известен как теорема Жуковского:

Если в соответствующие точки плана скоростей механизма приложить все активные силы и силы инерции, повернутые на 90º в одну сторону, то сумма моментов этих сил относительно полюса плана скоростей, рассматриваемого как жесткий рычаг, равна нулю.

На рис.3.8б представлен пример использования теоремы Жуковского для определения уравновешивающей силы в шарнирном четырехзвеннике.

В этом примере для правильного учета момента М он заменен парой сил (P' = P") так, что M = P₂^' L_AB. Уравновешивающая сила определяется из уравнения

P_ур h_ур + P₂'h_p2' + P₂ h_p2" + G₃ h_G3 + Q h_Q = 0.

При составлении уравнения должно соблюдаться правило знаков: момент, действующий против часовой стрелки, - положительный, по часовой стрелке – отрицательный.

Можно повернуть план скоростей, а силы не поворачивать, результат будет тот же.

3.9. Аналитический метод силового исследования

Известно несколько аналитических методов силового исследования. Познакомимся с методом, в основе которого также лежит принцип возможных перемещений. Для шарнирного четырехзвенника, нагруженного только уравновешивающим моментом М_ур и моментом сил полезного сопротивления M_Q, уравнение равновесия имеет вид:

M_ур δφ₁ + M_Q δφ₃ = 0,

откуда следует

M_ур = - M_Q δφ₃ / δφ₁ . (3.6)

Задача сводится к чисто кинематической: нужно выразить δφ₃ через δφ₁ и подставить в уравнение (3.6). Зависимость δφ₃ от δφ₁ устанавливается при решении задачи о скоростях.

Точно также можно учитывать действие других сил. При одновременном приложении нескольких сил уравновешивающий момент равен сумме моментов, рассчитанных для отдельных сил. В этом проявляется принцип суперпозиции – независимости действия сил.

Аналитический метод, в отличие от графического, можно применять и для пространственных механизмов. Расчет, вследствие сложности расчетов, производится с использованием вычислительных машин.

3.10. Задача уравновешивания ротора

Ротором называется звено механизма, выполненное в виде тела вращения и установленное в опорах на стойке. В связи с ростом рабочих скоростей машин уравновешиванию роторов придается большое значение. Уравновешивание представляет ответственный этап при изготовлении машин. Качество машины во многом определяется ее уравновешенностью. В настоящее время строятся электродвигатели и турбомашины со скоростью вращения 100000 оборотов в минуту, центрифуги для получения биологических эмульсий со скоростью вращения до 600000 оборотов в минуту, отдельные детали в текстильных машинах вращаются со скоростью до 1000000 оборотов в минуту.

Рассмотрим следующий пример: пусть масса ротора 10 кг, угловая скорость ω = 1000 рад/с, эксцентриситет массы 0.0001 м (0.1 мм). При вращении ротора возникает сила инерции U = mω²R = 1000 н, т.е. в 10 раз больше, чем вес ротора.

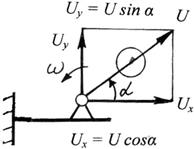
Рис 3.9. Действие неуравновешенного ротора на балку

Сила инерции передается на опоры в виде периодического воздействия. Пусть, например, неуравновешенный ротор закреплен на консольной балке (рис. 3.9). Разложим силу инерции U на составляющие U_x и U_y. Составляющая U_x из-за большой жесткости балки в направлении оси X не опасна, составляющая U_y вызывает колебания балки. Если частота вынужденных колебаний равна частоте свободных колебаний или ей кратна, может возникнуть резонанс. Резонанс характеризуется резким возрастанием амплитуды колебаний, что может привести к поломке или, в лучшем случае, будет проявляться в виде вибраций оборудования, здания и т.д.. Неуравновешенность может появиться также из-за неточности изготовления, пороков в материале и т. д. Задача конструктора – не допустить ошибок при проектировании ротора.

3.11. Статическая неуравновешенность ротора

Статической называется неуравновешенность, возникающая от того, что главная центральная ось инерции ротора проходит параллельно оси вращения. Свое название она получила потому, что она может быть обнаружена проведением статических испытаний. Рассмотрим простейшую схему статически неуравновешенного ротора (рис. 3.10). Подсчитаем силу инерции, развиваемую массой m

U = m ω² e.

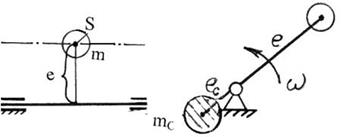
Рис 3.10. Схема статически неуравновешенного ротора

Силу инерции при угловой скорости ω = 1 называют дисбалансом:

D = U = m e.

Дисбаланс – произведение массы на эксцентриситет, его размерность гсм.

Задача уравновешивания – изменить распределение масс с тем, чтобы перевести центр масс на ось вращения. Тогда главная центральная ось инерции и ось вращения совпадут. Этого можно добиться, если использовать корректирующую массу m_c, расположить ее на расстоянии е_с противоположно массе m так, чтобы она развивала силу инерции U_c = - U или D_c = - D. Отсюда следует, что для статической уравновешенности необходимо, чтобы геометрическая сумма дисбалансов равнялась нулю

(D_c + D = 0).

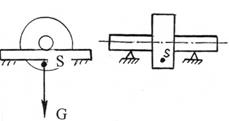
Рис 3.11. Балансировка ротора на параллелях

На практике статическое уравновешивание выполняют на балансировочных станках. Обычно используются балансировочные параллели (рис. 3.11) Установленный на них ротор под действием момента сил тяжести совершает колебания относительно положения устойчивого равновесия, при котором центр масс находится в самом нижнем положении. Ротор ведет себя как физический маятник. После прекращения колебаний определяется линия, на которой находится центр масс – «тяжелое место». С противоположной стороны закрепляется пробный грузик и испытание повторяется. Ротор будет уравновешен, если он будет находиться в состоянии безразличного равновесия.

Достоинство такого метода уравновешивания – простота оборудования. Недостаток – низкая точность из-за наличия трения качения. Остаточный дисбаланс рассчитывается по формуле

D_ост = m k,

где k - коэффициент трения качения.

Второй недостаток состоит в том, что таким способом нельзя обнаружить моментную неуравновешенность.

3.12. Моментная неуравновешенность ротора

Схема ротора с моментной неуравновешенностью представлена на рис. 3.12а. В том случае, если D₁ = - D₂, ротор статически уравновешен, однако дисбалансы, располагаясь на плече L, создадут момент M = D L, который будет воздействовать на опоры, вызывая в них реакции R_A и R_{B .} Такая неуравновешенность возникает, например, если отверстие в детали просверлено под углом к оси вращения (рис. 3.12б).

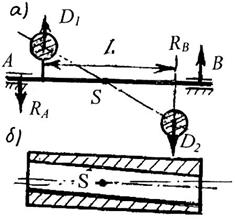
Рис 3.12. Схема ротора с моментной неуравновешенностью

Моментной называется неуравновешенность, возникающая оттого, что главная центральная ось инерции пересекает ось вращения в центре масс.

Для моментного уравновешивания необходимо добавить две корректирующие масс, такие, чтобы они создали момент дисбаланса M_m = - M. Геометрическая сумма моментов всех дисбалансов должна быть равна нулю.

Моментное уравновешивание производится на специальных станках. Такому уравновешиванию подвергаются детали большой протяженности вдоль оси. Для деталей типа зубчатых колес, шкивов, маховиков, автомобильных колес достаточно ограничиться статическим уравновешиванием.

3.13. Полное уравновешивание ротора с известным расположением масс

Статическое и моментное уравновешивание называют полным (динамическим) уравновешиванием. Рассмотрим его на примере коленчатого вала двигателя (рис. 3.13).

Уравновешивание будем производить в такой последовательности: сначала моментное, а затем статическое.

Запишем условие моментной уравновешенности:

M₁ + M₂ + M₃ + M_M = 0. (3.7)

Здесь

M₁ = D₁ L₁ = m₁ e₁ L₁ ;

M₂ = D₂ L₂ = m₂ e₂ L₂;

M₃ = D₃ L₃ = m₃ e₃ L₃.

Направление векторов моментов примем совпадающим с направлением векторов дисбалансов. Из уравнения (3.7) предстоит определить М_{М .} Решение уравнения получим построением многоугольника моментов.

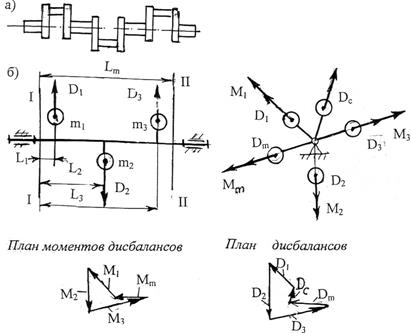
Рис 3.13. Полное уравновешивание ротора

Из построенного многоугольника моментов с помощью масштабного коэффициента определяем момент дополнительного дисбаланса М_М, который следует приложить к ротору, чтобы уравновесить его моментно.

M_M = D_M L_M = m_M e_M L_M .

Отсюда, задавшись L_M и e_M, находим m_M. Корректирующую массу m_M следует расположить в плоскости II – II на расстоянии e_M от оси вращения в направлении, указанном вектором М_М на многоугольнике моментов.

Условие статической уравновешенности:

D₁ + D₂ +D₃ + D_M + D_c = 0.

Построим в масштабе k_D многоугольник дисбалансов, из которого найдем величину и направление D_c: D_c = m_c e_c. Корректирующую массу m_c следует расположить в плоскости I – I на расстоянии e_c от оси вращения в направлении, указанном для D_c на многоугольнике дисбалансов.

Таким образом, с помощью двух масс произведено полное уравновешивание ротора.

3.14. Балансировка на машинах

Уравновешивание на стадии проектирования не дает гарантии, что изготовленная деталь будет уравновешена. Ошибки возможны при изготовлении. Для их исправления все ответственные детали подвергаются балансировке на машинах. Конструкции машин весьма разнообразны, рассмотрим простейшую схему машины (рис. 3.14).

Рис 3.14. Балансировочная машина

Ротор запускается через фрикционную передачу в зарезонансный режим, а затем двигатель отключается. При прохождении резонанса возникают колебания рамы, которые регистрируются измерительным прибором И. Плоскость II – II проходит через ось качания С. Благодаря этому сила инерции в плоскости II – II уравновешивается реакцией R_C. Сила инерции в плоскости I – I вызывает колебания рамы. Используя корректирующие грузы, добиваются уравновешивания сил инерции в плоскости I – I, а затем ротор переворачивается так, чтобы плоскость I – I прошла через точку С и добиваются уравновешивания в плоскости II – II. Процесс уравновешивания является трудоемким, так как требует многократных запусков ротора.

3.15. Уравновешивание механизмов

Уравновешивание механизмов производится с теми же целями, что и уравновешивание роторов. При работе механизмов возникают динамические реакции, которые могут значительно превышать статические реакции. От статических реакций избавиться нельзя, динамических можно избежать, если произвести уравновешивание механизма.

Полное уравновешивание механизма будет тогда, когда ускорение центра тяжести всего механизма равно нулю и момент сил инерции тоже равен нулю. Избежать воздействия момента сил инерции не удается, но добиться, чтобы ускорение центра масс было равно нулю, можно – нужно сделать так, чтобы он был неподвижен. При решении этой задачи используют метод замещающих масс.

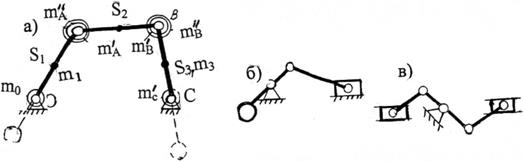
Рис 3.15. Уравновешивание четырехзвенника и кривошипно-ползунного механизма

Пусть, например, требуется уравновесить плоский шарнирный четырехзвенник (рис. 3.15). Заменим массу m двумя массами m_O и m_A^', поместим их в точки О и А, соблюдая условия

м_O OS₁ = m_A^'AS₁, (3.8)

м_O + m_A^' = m ₁.

Уравнения (3.8) образуют линейную систему относительно m_O и m_A^', решение которой находится элементарно.

Аналогичным образом заменяется масса m₃ и масса m₂ :

m_C = m₃ BS₃ / BC; m_B' = m₃ CS₃ / BC

; m_A^" = m₂ BS₂ / AB; m_B" = m₂ AS₂ / AB.

Итак, в точке А сосредоточена масса m_A = m_A' + m_A", в точке В сосредоточена масса m_B = m_B' + m_B". Массы в точках А и С уравновешены. Следует уравновесить массы m_A и m_B. Это достигается установкой дополнительных противовесов на звеньях ОА и ВС. Расчет их производится известным методом. Подобным же образом производится уравновешивание кривошипно-ползунного механизма, однако здесь остается неуравновешенной поступательно движущаяся масса ползуна. Полностью уравновешен механизм, составленный из двух кривошипно-ползунных механизмов, работающих в противофазе. Хорошо уравновешены многоцилиндровые двигатели внутреннего сгорания, хуже всех – одноцилиндровые двухтактные двигатели.

3.16. Силы трения в механизмах. Законы трения

Уточненный силовой расчет ведется с учетом сил трения. Сила трения, является результатом взаимодействия двух тел, она тоже относится к реактивным силам. Эта сила направлена касательно к поверхностям соприкасающихся тел и препятствует движению одного тела относительно другого. Физическая природа этой силы связана с деформацией микронеровностей и наличием сил молекулярного взаимодействия. Трение такого рода называется трением скольжения. Несмотря на то, что трение есть одно из самых распространенных явлений природы, точные законы трения до сих пор не установлены из-за многочисленности факторов, определяющих трение. Поэтому используются приближенные законы, которые пригодны для большинства практических задач. Эти законы установлены Амонтоном и Кулоном.

1. Сила трения пропорциональна нормальному давлению и направлена противоположно направлению относительной скорости.

F = f N.

Коэффициент пропорциональности f называется коэффициентом трения. Поскольку для двух трущихся тел можно указать две относительные скорости V_ij и V_{ji ,}, соответственно существуют две силы трения F_ij и F_ji, которые равны по величине и противоположны по направлению. Силы трения представляют касательные реакции для взаимодействующих тел.

2. Коэффициент трения зависит от материалов и состояния поверхностей трущихся тел. С уменьшением микронеровностей трение уменьшается. Экспериментально установлены следующие коэффициенты трения для наиболее характерных пар материалов:

сталь по стали - 0.18;

чугун по стали 0.20;

сталь по дереву 0.40;

ферродо по металлу 0.3 – 0.8;

резина по стали 0.6 – 0.8;

дерево по дереву 0.4 – 0.7.

3. Коэффициент трения зависит от скорости движения: сначала несколько убывает, а затем сохраняет почти постоянное значение.

4. Сила трения не зависит от удельного давления, а это значит – от площади контакта тел.

5. Коэффициент трения при движении (динамический коэффициент трения) меньше коэффициента трения при покое (статический коэффициент трения).

3.17.Трение в поступательной паре

На рис. 3.16,а представлена схема поступательной пары. Пусть к ползуну приложена сила Q, направленная перпендикулярно направляющей, и движущая сила P. Со стороны направляющей на ползун действуют нормальная реакция N и сила трения F, являющаяся касательной реакцией. Геометрическая сумма N и F есть полная реакция R. Угол между R и N назовем углом трения, поскольку он зависит от силы трения F. При равномерном движении ползуна соблюдается условие P = F, где F = f N, откуда следует f = F / N. Из построения на рис. 3.16,а следует, что F / N = tg φ где φ = arctg f. При малом коэффициенте трения φ ≈ f. Так, например, при f = 0.2 φ = 0.2 рад ≈ 12˚.

Коэффициент трения определяется экспериментально на установке, схема которой показана на рис. 3.16,б. На плоскости, наклоненной к горизонту под углом α помещено тело. Установим условия, при которых тело будет покоиться на плоскости.

Рис 3.16. Трение в поступательной паре

Разложим силу тяжести на две составляющие – по нормали и по касательной к поверхности. Нормальная составляющая, равная G cos α, прижимает тело к плоскости, касательная составляющая, равная G sin α, стремится сдвинуть тело вниз по плоскости, Этой силе противодействует сила трения F = f G sin α. Условие равновесия тела на плоскости

F≥ G sin α

или

FG cos α ≥ G sin α f ≥ tg α tgφ ≥tg α φ ≥ α.

Равновесие тела на наклонной плоскости не зависит от величины силы. Такое состояние носит название самоторможения. Самоторможение часто используется в грузоподъемных механизмах.

Явление самоторможения наблюдается в поступательной паре, если к ползуну приложена сила Р под углом меньшим угла трения (рис. 3.13в). Доказательство этого то же, что и для тела на наклонной плоскости. Угол трения определяет конус трения. Если сила трения приложена внутри конуса трения, то она не может сдвинуть тело с места. Это следует учитывать при проектировании механизмов с поступательными парами.

Установленные зависимости используются для анализа трения в резьбе. На рис. 3.17 показан один виток прямоугольной резьбы. Согласно 3-му закону трения гайку можно заменить небольшим элементом, нагруженным теми же силами, что и гайка. В таком случае возникает аналогия с ползуном, перемещающимся по наклонной плоскости, где α – угол подъема винтовой нарезки.

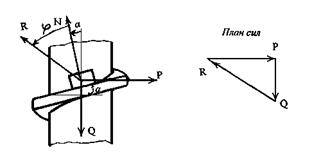
Рис 3.17. Трение в резьбе

Построим треугольник сил, приложенных к ползуну. Из треугольника следует

P = Q tg (α + φ).

Момент, который необходимо приложить к гайке, чтобы преодолеть силу Q, равен

M = P r_ср = Q r_ср tg (α+ φ),

где r _ср - средний радиус резьбы.

Угол подъема α обычно принимается небольшим для обеспечения самоторможения гайки, угол трения φ = arc tg f₀, где f₀ - приведенный коэффициент трения. Для прямоугольной резьбы f₀ = f, для треугольной резьбы f₀ = f / cos 30˚.

3.18.Трение во вращательной паре.

Вращательная пара состоит из втулки и цапфы. Если к цапфе приложен движущий момент, она будет перекатываться по цилиндрической поверхности втулки до тех пор, пока реактивный момент не уравновесит движущий момент. На рис. 3.18 представлено положение равновесия цапфы. Из проекции всех сил на ось Y следует, что Q = - R, где Q - вертикальная нагрузка, R - полная реакция, Q и R образуют пару сил с плечом ρ, где ρ – радиус круга трения.

M_тр = Q ρ.

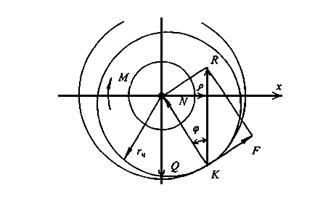
Рис.3.18. Трение во вращательной паре

Из построения на рис. 3.18 видно, что ρ = r_ц sin φ.

Поскольку sin φ ≈ tg φ, при малых значениях φ

M_тр = Q r_ц tg φ = Q r_ц f.

Коэффициент трения f для вращательной пары определяется экспериментально. Обычно он на 30% больше, чем для поступательной пары.

Здесь рассмотрен упрощенный подход к определению трения во вращательной паре, не учитывающий реального распределения удельного давления на поверхности кинематической пары. При более строгом подходе рассматриваются две гипотезы распределения давления, так называемые гипотеза постоянного давления и гипотеза постоянного износа. Первая относится к новым цапфам, а вторая – к приработавшимся цапфам. В результате получаются формулы, аналогичные вышезаписанным с приведенным коэффициентом трения 1.27 f для приработавшихся цапф и 1.47f для новых.

3.19. Трение в высшей паре.

В высшей кинематической паре имеет место скольжение и качение элементов друг по другу. Сила трения скольжения вычисляется также как и в поступательной паре. Сопротивление перекатыванию учитывается моментом трения качения, который направлен противоположно угловой скорости.

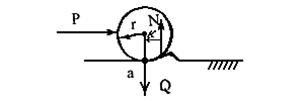
Рис 3.19. К определению трения качения в высшей паре

Физическая природа трения качения изучена недостаточно, поэтому обычно пользуются экспериментальными данными. При качении тела затрачивается работа, которая идет на деформацию поверхностей качения. Пусть, например, перекатывается цилиндр по плоскости (рис. 3.19). Перед цилиндром образуется волна деформации, которая движется вместе с ним. Равнодействующая элементарных реакций смещена от точки а на величину k. Для качения цилиндра необходимо преодолеть момент М_тр = kN = k Q, где Q – сила, приложенная к телу. Коэффициент пропорциональности в этой формуле, по аналогии с законом трения на плоскости, называют коэффициентом трения качения.

3.20. Динамический анализ механизмов. Приведение сил и масс.

Для того, чтобы выполнить силовое исследование, необходимо знать закон движения начального звена. Он устанавливается при решении задачи об истинном движении механизма. В этой задаче активные силы считаются известными, составляется уравнение, связывающее силы и ускорения, а затем путем их интегрирования находится скорость и перемещение как функции времени. Основные трудности здесь чисто математического характера. Они вызваны сложностью интегрирования нелинейного дифференциального уравнения. С целью упрощения записи дифференциального уравнения рассматривается одномассовая динамическая модель механизма. Вместо движения всего механизма изучается движение одного звена, так называемого звена приведения. Обычно за звено приведения выбирается начальное звено механизма. Для того, чтобы такая замена была возможна, необходимо, чтобы звено приведения было динамически эквивалентно всему механизму.

Условие динамической эквивалентности состоит в следующем: во – первых, кинетическая энергия звена приведения должна равняться кинетической энергии механизма; во – вторых, работа силы, приложенной к звену приведения, на возможном перемещении должна равняться сумме работ всех сил, приложенных к механизму, на их возможных перемещениях. Указанное условие вытекает из того, что при составлении уравнения движения механизма в расчет принимается только закон изменения кинетической энергии и внешних сил, а не реальная схема механизма. При такой замене и для механизма и для звена приведения справедливо одно и то же уравнение.

Не нашли, что искали? Воспользуйтесь поиском: