Другие виды зацепления 2 страница

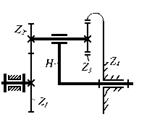
Рис. 5.36. Схема планетарного механизма

1. Определяем передаточное отношение соответствующего обращенного механизма:

i₁₄^H =1 – i_1H = - 11.

2.Разложим полученное передаточное отношение на множители. Здесь возможны разнообразные варианты, например:

i₁₄^H = Z₂ Z₄ / Z₁ Z₃ = 220 / 20 =4 ▪ 55 / 4 ▪ 5.

3.Запишем условие соосности и проверим его выполнение для принятых чисел зубьев:

Z₁ + Z₂ = 4 + 4 = 8,

Z₄ – Z₃ = 55 – 5 = 50.

4.Условие соосности, как правило, не выполняется. Для его выполнения нужно умножить верхнюю формулу на 50, а нижнюю – на 8. Тогда

Z₁ = 200, Z₂ = 200, Z₄ = 440, Z₃ = 40.

Полученные числа зубьев можно сократить так, чтобы получились реально выполнимые колеса с числом зубьев в пределах 10 – 100.

5.31. Волновая передача

В 1959 году Массер (США) запатентовал зубчатую передачу, которая в настоящее время пользуется большой популярностью. Ее основные достоинства – большое передаточное отношение, высокий к.п.д., способность передавать движение в герметичные полости, многопарность зацепления (до 30% зубьев), малое скольжение и износ.

В волновой передаче одно из колес выполняется гибким, способным деформироваться под действием звена, называемого генератором волн. Волновые передачи весьма разнообразны. Чаще всего они выполняются с неподвижным жестким звеном и внутренним гибким колесом. Возможны двухволновые и многоволновые механизмы с генератором в виде эллипсовидного звена с шариковым подшипником. Преобразование движения происходит за счет деформации упругой оболочки.

Легче всего принцип действия волновой передачи объяснить, исходя из аналогии с планетарной передачей. Волновая передача, представленная на рис. 5.37,а эквивалентна двухколесной планетарной передаче (рис. 5.37, б), у которой число зубьев сателлита равно числу зубьев гибкого колеса.

Для планетарного механизма

i₁₂^H = (ω₁ – ω_H) / (ω₂ – ω_H) = Z₂ / Z₁;

ω₁ / ω_H = 1 – Z₂ / Z₁;

i_пл = ω_H / ω₁ = 1 / (1 – Z₂ / Z₁).

Если Z₂ / Z₁ ≈ 1, то i _пл получается очень большим и имеет отрицательный знак.

Еще один вариант исполнения волновой передачи представлен на рис. 5.37 в. Здесь посредством гибкой стенки герметично разъединены полости А и Б Планетарным аналогом служит механизм с поступательно движущимся сателлитом. Для него

i₁₂^H = (ω₁ – ω_H) / (ω₂ – ω_H) = Z₂ / Z₁;

i_2H = ω₂ / ω₁ = 1 – i₂₁^H;

i_пл = ω_H / ω₂ = (Z₂ / Z₁) / (Z₂/ Z₁ – 1).

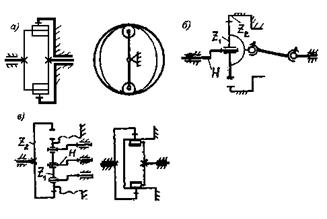
Рис. 5.37. Волновые передачи

Здесь передаточное отношение положительно, что обусловливает большой к.п.д. Одним из достоинств волновой передачи является высокий к.п.д. Это обусловливает его применение в тех случаях, когда экономия энергии чрезвычайно необходима, например, в космической технике.

5.32. Планетарные механизмы робототехнического назначения

Планетарные механизмы находят широкое применение в различных робототехнических устройствах. В некоторых случаях они обеспечивают основные движения роботов, как например механизм ориентации кисти робота. В основе его использован зубчатый дифференциальный механизм с коническими колесами.

Для объяснения принципа работы этих достаточно своеобразных механизмов рассмотрим вначале схему простейшего конического дифференциала (рис. 5.38,а).

Угловая скорость колеса 2 находится из соотношения

,

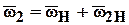где 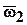и 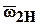– векторы абсолютной угловой скорости соответствен­но для колеса 2 и водила Н; 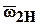– вектор угловой скорости звена 2 отно­сительно водила.

Сообщим обращенное движение всему механизму вокруг колеса 1 со скоростью водила, но в противоположном направлении. Это очевидно не изменит относительного движения звеньев, однако позволит рассматри­вать обращенный механизм как рядовую коническую передачу (рис. 5.38,6).

Для нее справедливо выражение

, (5.16)

где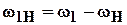

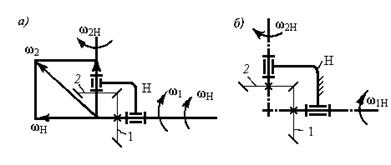
Рис. 5.38. Двухколесный конический дифференциал (а) и

его обра­щенная схема (б).

Анализ формулы (5.16) показывает, что при

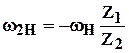– механизм планетарный;

при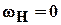

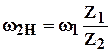– механизм рядовой.

Конический дифференциал применяется в кисти робота. Из приве­денных выше соотношений вытекает, что при качании кисти имеет место и ее ротация, т. е. поворот вокруг собственной оси. Чтобы разделить эти

движения, следует сообщить центральному колесу 1 угловую скорость .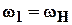

Уравнение кинематической связи для симметричного конического дифференциала (рис. 5.39), также широко применяемого в роботах, име­ет вид

.

Из него следует, что если скорости центральных колес одинаковы, дифференциал заблокирован , а если одно из центральных колес неподвижно, , т.е. скорость водила равна половине ско­рости ведущего колеса при том же направлении вращения.

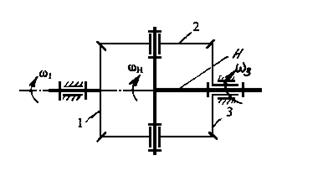
Рис. 5.39. Симметричный конический дифференциал

Для преобразования вращательного движения в поступательное применяется реечная зубчатая передача, представляющая по существу ва­риант зубчатой передачи, у которой зубчатое колесо имеет бесконечно большой радиус.

Реечные передачи могут выполняться и по дифференциальным схе­мам

Линейные скорости точек механизма (рис. 5.40) связаны соотношением V_A=V_H+V_AH, (5.17)

где V_H – скорость водила; V_AH – скорость точки А относительно во­дила.

Сообщим механизму обращенное поступательное движение со ско­ростью – V_H. Для обращенного механизма

V_AH=V_A-V_H=-(V_B–V_H). (5.18)

После подстановки выражения (5.18) в (5.17) получим уравнение реечного дифференциала

V_A=2V_H -V_B.

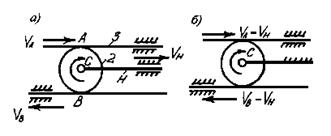
Рис. 5.40. Реечный дифференциал (а) и его обращённая схема (б)

Если скорость точки В равна нулю, то V_A = 2Vh, т.е. происходит удвоение скорости водила, а значит ход звена 3 в два раза больше хода водила.

В роботах находит применение планетарный механизм с гибким тяговым органом, в качестве которого может служить цепь. Цепь охватыва­ет неподвижную звездочку 1 и подвижную звездочку 2, закрепленную на несущем подвижном звене (рис. 5.41,а).

Звездочка 2 здесь играет роль сателлита, а несущее подвижное звено – роль водила. При вращении водила с угловой скоростью 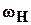сателлит из-за наличия гибкой связи приобретает абсолютную угловую скорость направлении противоположном вращению водила.

Применим принцип обращения движения и рассмотрим образовав­шийся механизм (рис. 5. 41,б). Это рядовая цепная передача, для которой кинематическое уравнение имеет вид

,

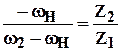откуда следует уравнение для планетарного механизма:

.

Пусть, например, 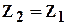,тогда и звездочка 2 при движении водила сохраняет ориентацию неизменной. Если же , то .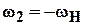

Рис. 5.41. Цепной планетарный механизм

Оба механизма используются в манипуляторах: первый – для развяз­ки вращательных движений; второй – для получения прямолинейного движения за счет использования двух звеньев равной длины, вращающих­ся с одинаковыми скоростями, но в противоположных направлениях.

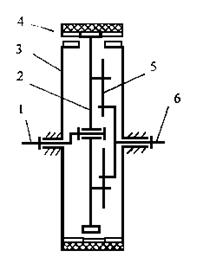
Рнс.5.42.Зубчато-ременный планетарный редуктор: 1– входной вал,

2 – подвижный шкив, 3 – неподвижный шкив-звездочка, 4 – зубчатый ре­мень, 5 – крестовая муфта, 6 – выходной вал.

На основе описанного выше цепного планетарного механизма авто­ром этого пособия разработан зубчато-ременный планетарный редуктор. Кинематика этого редуктора полностью описывается приведенными выше формулами. Его достоинства – малые габариты при больших передаточ­ных отношениях благодаря тому, что разность чисел зубьев зубчатых шки­вов 2 и 3 равна единице. Кроме того, из-за использования зубчатого ремня уменьшен шум передачи и уменьшена масса по сравнению с плане­тарными механизмами обычного типа.

Из-за наличия большого числа зубьев, находящихся в зацеплении, повышается нагрузочная способность передачи. Благодаря использованию в передаче ремня уменьшается момент инерции подвижных частей, а значит улучшаются динамические характеристики привода. Ремень изготавливается из резины или полиуретана. Ременная передача может работать в условиях отсутствия смазки.

Контрольные вопросы.

1. Охарактеризуйте достоинства зубчатых механизмов

2. Какие передачи относятся к классу гиперболоидных передач?

3. В чем состоит основной закон зацепления?

4. Какими основными свойствами обладает эвольвента окружности?

5. В чем состоят преимущества эвольвентного зацепления перед другими видами зацепления?

6. Назовите два метода нарезания колес. Охарактеризуйте их особенности.

7. Что такое смещение?

8. Что такое делительная окружность? Какие еще окружности можно указать на зубчатом колесе?

9. Какие качественные характеристики зацепления, можно определить с помощью картины зацепления?

10. На что указывает коэффициент перекрытия?

11. В чем преимущества косозубых колес?

12. Что такое передаточное отношение? Как оно выражается через

числа зубьев колес для рядового зубчатого механизма?

13. В чем состоит отличие планетарного механизма от рядового?

Какие названия имеют его звенья и почему?

14. Приведите пример дифференциального механизма.

6. СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ

6.1. Виды кулачковых механизмов

Кулачковым механизмом называется механизм, в состав которого входит кулачок ( звено, рабочая поверхность которого имеет переменную кривизну). Зубчатый механизм можно рассматривать как многокулачковый механизм.

Кулачковые механизмы широко применяются в двигателях внутреннего сгорания, в текстильных машинах, в полиграфических машинах, в машинах – автоматах различного назначения, в разнообразных приборах. Достоинство кулачковых механизмов – возможность воспроизводить почти любой закон движения, причем синтез их относительно несложен. Недостатки – наличие высшей кинематической пары и, как следствие, ограниченная долговечность, сложность изготовления, высокая стоимость.

Кулачковый механизм состоит из кулачка (обычно вращающегося) и толкателя, совершающего возвратно – поступательное движение. Иногда толкатель совершает колебательное движение, в таком случае он называется коромыслом. Для уменьшения трения толкатель снабжают роликом. Схемы кулачковых механизмов чрезвычайно разнообразны. Кулачковые механизмы бывают плоские и пространственные, с толкателем или коромыслом, имеющим в качестве рабочего элемента острие, ролик или плоскость, центральные и дезаксиальные (рис. 6.1).

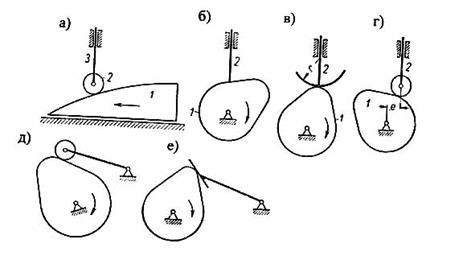
Рис. 6.1. Виды кулачковых механизмов

Соприкосновение звеньев в кулачковом механизме обеспечивается силовым или геометрическим замыканием (рис. 6.2). Силовое замыкание

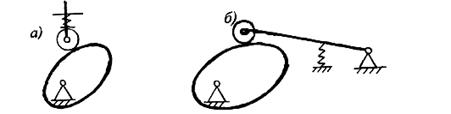
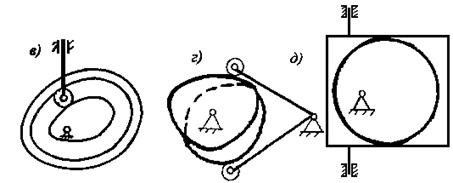
Рис.6.2. Силовое и геометрическое замыкание

осуществляется с помощью пружины. Геометрическое замыкание осуществляется с помощью паза, в котором помещается ролик толкателя. Недостатком такой конструкции является трудоемкость точного выполнения паза и наличие удара при реверсировании движения толкателя из-за неизбежного зазора между роликом и пазом. От этого недостатка свободен двухдисковый кулачок. Еще одну разновидность представляет диаметральный кулачок с рамочным толкателем.

6.2. Заменяющие механизмы

Кулачковый механизм может быть заменен кинематически эквивалентным рычажным механизмом. В основе такой замены лежит принцип замены механизма с высшей парой механизмом с низшими парами: через точку касания элементов высшей пары следует провести общую нормаль к профилям, в центрах кривизны профилей поместить шарниры или поступательные пары (если одним из профилей является прямая линия).

На рис. 6.3 представлены кулачковые механизмы и заменяющие их рычажные механизмы: шарнирный четырехзвенник, кривошипно-ползунный, синусный механизм.

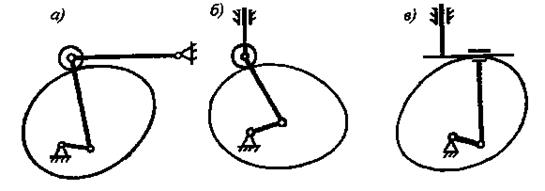
Рис.6.3. Заменяющие механизмы

Движение ведомых звеньев будет одинаковым в кулачковых и заменяющих их рычажных механизмах. Следует подчеркнуть, что речь идет о мгновенно заменяющих механизмах, так как в связи с непрерывным изменением радиуса кривизны кулачка меняется длина кривошипа и шатуна. Таким образом, задачу кинематического исследования кулачкового механизма можно свести к исследованию соответствующего рычажного механизма.

6.3. Элементы профиля кулачка

Несмотря на чрезвычайное разнообразие профилей кулачков можно указать общие для всех их элементы. Для всякого кулачка можно найти точки, наиболее и наименее удаленные от центра вращения, и указать соответствующие им максимальный радиус R_max и минимальный радиус R_min (рис. 6.4). Окружность радиусом R_min называется окружностью минимального радиуса. Она играет важную роль при последующем анализе кулачковых механизмов. В моменты, когда толкатель контактирует с точками профиля, соответствующими R_min и R_max, он неподвижен. Если такая точка одна, то толкатель совершает мгновенную остановку, если таких точек много, так, что они образуют дугу радиуса R_min или R_max, имеет место нижний или верхний выстой.

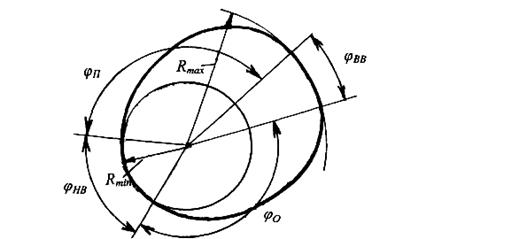
Рис. 6.4. Элементы профиля кулачка

Между периодами остановок (выстоев) лежат периоды подъема и опускания толкателя. Они соответствуют левому и правому рабочим профилям кулачка. Именно рабочий профиль определяет закон перемещения толкателя при подъеме или опускании. Соответствующие периоды называются фазами работы толкателя и на профиле кулачка определяются фазовыми углами: углом нижнего выстоя φ_нв, углом подьема φп, углом верхнего выстоя φвв, углом опускания φ_о.

Фазовые углы связаны соотношением: φ_п + φ_вв + φ_о + φ_нв = 360˚.

Для любого кулачкового механизма диаграмма перемещений толкателя имеет характерный вид, представленный на рис.6.5

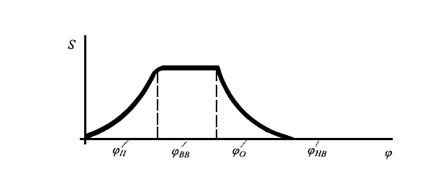
Рис. 6.5. Диаграмма перемещений

Разнообразие законов движения достигается за счет различного сочетания длительностей фаз, а также различных законов подъема и опускания толкателя.

6.4. Выбор закона движения толкателя

В ряде технологических машин, таких как текстильные, полиграфические и другие, закон движения полностью определен той операцией, для выполнения которой механизм предназначен. В таком случае выбор закона движения отпадает. Однако во многих случаях, например, в машинах – автоматах, автомобильных двигателях, технологическим процессом задаются только фазовые углы и величины перемещений. Внутри каждой фазы подъема и опускания закон движения может быть произвольным, тогда закон движения выбирается таким, чтобы механизм был оптимальным в динамическом отношении.

Простейшим законом является закон постоянной скорости (рис. 6.6). Скорость в точке 1 теоретически мгновенно изменяет направление, следовательно ускорение стремится к бесконечности. Практически из – за упругости звеньев изменение направления происходит за некоторый малый промежуток времени, поэтому ускорение не бесконечно, но велико, а,следовательно, и очень велика сила инерции. Это явление носит название жесткого удара. Такой закон движения может быть применен только для малоответственных тихоходных механизмов.

Рис. 6.6. Законы движения толкателя

Жесткого удара можно избежать, если принять закон постоянного ускорения. Однако здесь мгновенно изменяется направление ускорения и, следовательно, – направление силы инерции. Это тоже проявляется в виде удара – “ мягкого удара”, который приводит к колебаниям и дополнительным динамическим нагрузкам. При применении закона косинусоидального ускорения в точке 1 сила инерции равна нулю, но мягкий удар в точке 2 все же происходит, если далее следует выстой толкателя.

Безударными будут синусоидальный закон и полиноминальный закон. Однако применение двух последних законов предъявляет очень высокие требования к точности изготовления кулачков.

Раньше обычно применялись кулачки, очерченные дугами сопряженных окружностей. Несмотря на то, что профиль таких кулачков

был абсолютно гладким, в точках сопряжения происходили мягкие

удары, так как имело место мгновенное изменение радиусов кривизны.

6.5. Изготовление кулачков

Кулачковые механизмы очень чувствительны к точности профиля кулачка. Поэтому они требуют особо тщательного изготовления. Основной метод изготовления кулачков – по точкам. На требуемом расстоянии от оси кулачка устанавливается фреза и производится обработка элемента профиля. Затем заготовка с помощью делительного устройства поворачивается на 0.5 – 1˚, фреза устанавливается в новое положение и так далее. Процесс очень трудоемок, так как требует большого числа установок. Возникающие при таком способе изготовления гребешки на профиле удаляются при последующей доработке. Для изготовления кулачков применяются также копировально-фрезерные станки и станки с числовым программным управлением. Профиль кулачка задается в числовом виде и автоматически воспроизводится на заготовке.

6.6. Анализ кулачковых механизмов

Анализ кулачкового механизма состоит в определении кинематических параметров движения толкателя: перемещения, скорости и ускорения. Рассмотрим эту задачу на примере центрального кулачкового механизма с толкателем, имеющим острие (рис. 6.7).

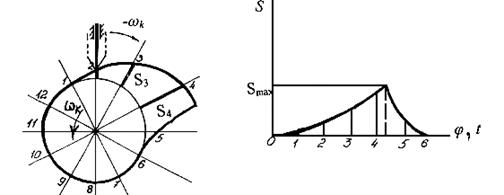
Рис. 6.7. Анализ кулачкового механизма

Как видно из рисунка, для данного положения кулачкового механизма перемещение толкателя есть разность между радиус – вектором профиля кулачка и окружностью минимального радиуса. Для определения перемещения в другом положении следует повернуть кулачок и снова найти эту разность. Однако с целью облегчения построений удобно сообщить механизму обращенное движение со скоростью равной скорости вращения кулачка, но в обратном направлении. В таком случае кулачок будет оставаться неподвижным, а ось толкателя будет занимать последовательные положения 1, 2, 3…

За начало отсчета принимают точку отрыва профиля кулачка от окружности минимального радиуса. Обычно окружность разбивают на 12 частей. Части берутся равными, так как согласно формуле φ = ω t, при постоянной скорости вращения углы поворота φ при равных интервалах времени тоже будут равными. Замерив перемещения и отложив их как ординаты, соединяют точки плавной кривой. Полученный график есть график s(φ) или в другом масштабе – график s(t). Графики v(t) и a(t) получаются графическим дифференцированием графика s(t).

Если толкатель снабжен роликом, то следует рассмотреть эквивалентный механизм, у которого центр ролика как острие работает по центровому профилю кулачка. Центровым профилем называется траектория ролика в обращенном движении. Центровой профиль является эквидистантным по отношению к действительному профилю. Расстояние между ними, измеренное по нормали к профилю, равно радиусу ролика.

Анализ кулачковых механизмов других видов принципиально подобен рассмотренному выше.

6.7. Угол давления и его связь с размерами кулачка

Более важную для практики и в то же время более сложную задачу представляет синтез кулачкового механизма. Синтез кулачковых механизмов выполняется в два этапа. Первый этап – определение основных размеров механизма: минимального радиуса, диаметра ролика, длины коромысла, положения неподвижных элементов механизма. Второй этап – определение профиля кулачка по заданному закону движения. Определение минимального радиуса кулачка производится на основании угла давления.

Углом давления называется угол между направлением силы и направлением перемещения, вызванного этой силой. В случае кулачкового механизма сила действует по общей нормали, проведенной через точку касания ролика и кулачка, направление перемещения – по оси толкателя (рис. 6.8).Угол θ между этими направлениями – угол давления.

Перенесем силу Р по линии действия n – n в точку В и разложим на составляющие N и T. Сила Т является движущей силой для толкателя, сила N прижимает толкатель к направляющей, в результате чего возникает сила трения F.

T = P cos θ N = P sin θ F = f N.

С увеличением угла θ движущая сила T уменьшается, а сила N, а значит и сила трения F, увеличивается. При некотором предельном значении угла θ движущая сила станет равной силе трения – толкатель застопорится.

F = T f P sin θ = P cos θ.

Отсюда tgθ = 1/f, т.е. предельный угол давления определяется коэффициентом трения f. В правильно спроектированном кулачковом механизме угол давления значительно меньше предельного.

Практика рекомендует допустимый угол давления до 30° для механизмов с роликовым толкателем и до 45° - для механизмов с роликовым коромыслом.

Выбирая соответствующие размеры кулачка, всегда можно удовлетворить поставленному требованию по углу давления. Выясни связь между размерами кулачка и углом давления Для этого рассмотрим эквивалентный исходному кулачковый механизм с острым толкателем, работающим по центровому профилю (см.рис. 6.8).

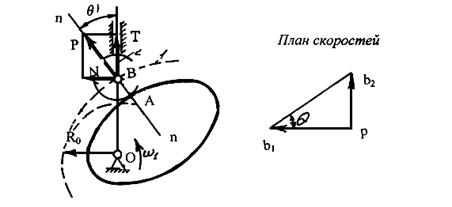
Рис. 6.8. Угол давления в кулачковом механизме

Построим план скоростей для этого механизма

V_b2 = V_b1 + V_{b2, b1} .

Из плана скоростей следует

tg θ = V_b2 / V_b1 = V_b/ ω (R_o + s). (6.1)

Из анализа этой формулы следует, что между углом давления и минимальным радиусом существует нелинейная связь, такая, что с увеличением минимального радиуса R_o угол давления уменьшается. Уменьшение угла давления благоприятно сказывается на к.п.д. механизма, однако это достигается за счет увеличения его габаритов.

На основании этой формулы разработан графический прием определения минимального радиуса (рис. 6.9), используемый обычно при курсовом проектировании.

Рис. 6.9.Определение минимального радиуса

Исходя из графиков движения толкателя s(t) и v(t) методом исключения общего переменного строится график v(s), а затем переходом к новой переменной 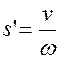– график 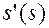. Переменная называется аналогом скорости. Положительное направление оси берется по направлению вращения кулачка. В связи с тем, что размерность s и одинакова, масштабные коэффициенты по обеим осям выбираются также одинаковыми.

Если от точки О вниз отложить минимальный радиус, а затем точку О₁ соединить линией с произвольной точкой 1 на графике, то эта линия образует с осью ординат угол θ – это вытекает из имеющегося соответствия отрезков на рис. 6.9 и формулы (6.1).

Максимальный угол давления получится, если из точки О₁ провести касательную к левой части графика. Для кулачка с силовым замыканием достаточно рассмотреть левую часть графика, так как опасность заклинивания существует только на фазе подъема.

6.8. Определение основных размеров кулачкового механизма с коромыслом

В основе определения минимального радиуса для кулачкового механизма с коромыслом также лежит рассмотренное выше соотношение между минимальным радиусом и углом давления. Различие заключается в своеобразии построения графика 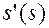, учитывающем непрерывное изменение направлений s и .

Угол давления для такого механизма определится как угол между направлением общей нормали n – n и вектором скорости V_B (рис. 6.10).

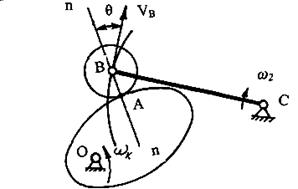
Рис. 6.10 Угол давления

Построение графика 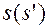выполняется следующим образом. В выбранном масштабе строятся крайние положения коромысла В₁С и В₂С. Дуга В₁В_{2 ,} представляющая траекторию точки В, делится на равные части, и через точки деления проводятся лучи из точки С. Для каждого положения коромысла соответствующий участок дуги и луч можно рассматривать как оси s и . Откладываем на лучах в принятом масштабе аналоги скорости , истинная величина которых рассчитывается по формуле

Не нашли, что искали? Воспользуйтесь поиском: