Q – сила полезного сопротивления. 4 страница

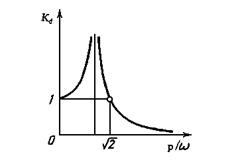
Рис.3.27. Зависимость коэффициента динамичности от р/ω

Уравнение (3.24) является уравнением движения колебательного типа. В таком случае силовой модуль представляет колебательную систему с одной степенью свободы.

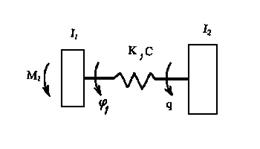
Рис.3.28. Двухмассовая динамическая модель

Колебательное движение накладывается на основное движение исполнительного звена, искажая его. Зная частоту и амплитуду колебаний, можно оценить точность его перемещения.

3.28. Характеристики упругих звеньев

При построении упругой модели манипулятора необходимо знать упругие характеристики его элементов. Как уже отмечалось, наибольшее значение имеют упругие свойства передаточных механизмов, в состав которых входят валы, зубчатые колеса, стержни, работающие на сжатие-растяжение, шпонки и шлицевые соединения и т.п.

Рассмотрим вал, работающий на кручение. Представим, что левый его конец закреплен, а к правому приложен крутящий момент М. Под действием этого момента правый конец вала повернется на угол закручивания 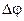. При малых деформациях угол 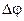пропорционален моменту М. Отношение называется коэффициентом жесткости (жесткостью) упругого вала, а - коэффициентом податливости (податливостью) вала. Для вала постоянного сечения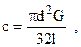

где - жесткость, 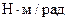; 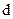— диаметр вала; 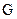— модуль сдвига, для стали 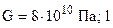— длина вала.

Податливость вала является величиной, обратной жесткости. Если вал ступенчатый, податливости складываются, а общая жесткость определяется как величина, обратная суммарной податливости. Так, например, для вала, имеющего два участка с коэффициентами жесткости и , общий коэффициент жесткости

Жесткость зубчатой передачи определяется следующим образом. Если закрепить ступицу шестерни, а к зубчатому колесу приложить момент 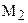, то вследствие контактной и изгибной деформации зубьев, а также деформации ободов обоих колес зубчатое колесо повернется на некоторый угол 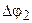. Отношение 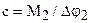называется жесткостью зубчатой передачи, приведенной к зубчатому колесу. Жесткость зубчатой передачи, приведенная к шестерне, в 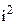раз меньше, так как , где — передаточное отношение от шестерни к колесу.

Для вычисления жесткости цилиндрической передачи можно пользоваться эмпирической формулой

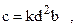
где с — жесткость, 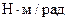; 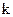— коэффициент пропорциональности, для стальных колес 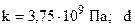— диаметр колеса, к которому приводится жесткость; 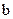— ширина зубчатого венца.

Жесткость зубчатых передач обычно намного выше жесткости валов, на которых они установлены.

Жесткость винтовой нарезки в продольном направлении определяется по формуле

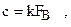
где с — жесткость, 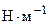; 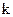— коэффициент пропорциональности, для стального винта и стальной гайки 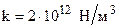; — площадь поверхности одного витка.

Жесткость стержня, работающего на растяжение-сжатие,

где с — жесткость, 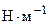; 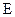- модуль продольной упругости, для стали 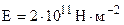; — площадь поперечного сечения; — длина стержня.

Жесткость упругих элементов — шпоночных соединений, муфт, цепных и реечных передач — можно найти в справочной литературе.

Для упрощения динамических моделей часто пользуются приемом приведения, заменяя системы звеньев, целые механизмы одним звеном — звеном приведения. Чтобы такая замена была возможна, звено приведения должно быть динамически эквивалентным заменяемому механизму.

Приведенным моментом инерции механизма называется условный момент инерции звена приведения, при котором его кинетическая энергия равна кинетической энергии всего механизма. Для зубчатого механизма (рис.3.26), у которого звеном приведения является звено 1, приведенный момент инерции определяется по формуле

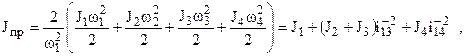
где 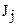- моменты инерции колес, включая моменты инерции валов; 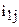- передаточные отношения от звена 1 к звену .

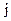Момент инерции зубчатого механизма — величина постоянная.

Рис. 3.29. Схема зубчатого механизма

Для плоской рычажной системы (рис. 3.27), которая может служить в качестве исполнительного органа манипулятора, приведенный момент инерции

где 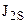- момент инерции звена 2 относительно центра масс; 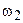- абсолютная угловая скорость звена 2; 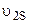- линейная скорость центра масс.

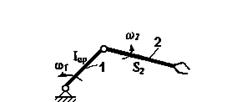
Рис. 3.30. Рычажный механизм

Приведенный момент инерции такого механизма – величина переменная, так как кинетическая энергия зависит от конфигурации системы.

Приведенным моментом называется условный момент, приложенный к звену приведения, работа которого на возможном перемещении равна сумме работ всех реальных внешних моментов, приложенных к звеньям на их возможных перемещениях. Очевидно, что для зубчатого механизма (см.рис.3.26), к выходному валу котрого приложен внешний момент 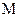, приведенный момент для звена приведения 1 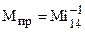, где - передаточное отношение. Здесь - постоянная величина. Для рычажного механизма (см.рис.3.27) приведенный момент зависит от конфигурации системы.

Приведенным коэффициентом жесткости 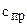механизма называется жесткость звена приведения, имеющего ту же потенциальную энергию, что и весь механизм. Для зубчатого механизма это условие имеет вид:

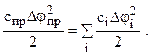
Пусть вал ротора двигателя (см.рис.3.26) закреплен, а к исполнительному звену приложен момент М. Вследствие податливости упругих элементов вал исполнительного звена повернется. Полный угол его поворота 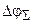равен сумме углов поворотов, вызываемых податливостью каждого упругого элемента, приведенных к валу исполнительного звена:

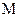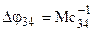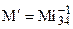Под действием внешнего момента вал 4—5 повернется относительно звена 4 на угол . Податливость зубчатой передачи 3—4 вызовет поворот колеса 4 на угол , где — жесткость зубчатой передачи, приведенная к валу колеса 4. Вал 2—3 нагружен моментом , где 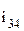— передаточное отношение зубчатой передачи 3—4. Под действием этого момента вал закрутится на угол 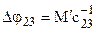, что вызовет поворот звена 5 на угол 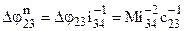. Рассматривая податливость зубчатой передачи 1 –2 и вала 0 –1, найдем приведенные углы поворота:

Произведя подстановку в выражение (3.25) находим полный угол поворота звена 5:

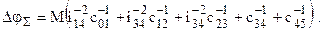
Жесткость механизма в целом, приведенная к валу исполнительного органа,

Отсюда следует, что податливость первых ступеней зубчатого механизма мало влияет на общую его податливость. Наибольшее значение имеет податливость элементов, ближайших к последней ступени редуктора и соединительного вала. Поэтому при конструировании зубчатых механизмов в первую очередь увеличивают жесткость выходных звеньев редуктора. Это служит объяснением тому, что при построении динамических моделей исполнительные звенья и редукторы считаются абсолютно жесткими, а податливость сосредоточивается в упругих соединительных валах.

В реальных механизмах всегда имеют место потери, связанные с внутренним трением, возникающим между микроэлементами материала при его деформировании, а также потери конструкционного демпфирования, вызванные трением на поверхности сопряжения деталей. Возникающие при этом силы трения называются диссипативными. Их значения пропорциональны скорости деформации элементов. Эти силы аналогичны силам, возникающим при движении тела в вязкой среде с малой скоростью при проталкивании движущимся телом жидкости через узкие каналы, как в случае амортизаторов. Поэтому силы трения, пропорциональные скоростям, принято называть силами вязкого трения или силами демпфирования. Для их определения вводятся коэффициенты вязкого трения, значения которых устанавливаются экспериментально.

Приведенный коэффициент вязкого трения для механизма в целом находится из условия равенства рассеивания энергии в отдельных упругих элементах рассеиванию энергии, которое имеет место в звене приведения. Зная коэффициенты вязкого трения упругих элементов, приведенный коэффициент можно определить по формуле, аналогичной выражению (3.26).

Контрольные вопросы

1. Какие задачи решает динамика машин?

2. Что такое сила инерции?

3. Как формулируется принцип Даламбера для механизмов? В чем состоит причина его использования при решении динамических задач для механизмов?

4. Как учитываются силы инерции при вращательном движении? Что такое момент инерции тела?

5. В чем состоит идея метода планов сил?

6. На чем базируется метод рычага Жуковского? Что на самом деле представляет этот рычаг?

7. Что такое ротор и почему его следует уравновешивать?

8. Как практически осуществляется балансировка роторов?

9. Какие законы трения принмаются во внимание при исследовании механизмов?

10. Что такое самоторможение и как оно проявляется в некоторых механизмах?

11. Что такое звено приведения механизма? Для чего вводится это понятие?

4. СИНТЕЗ РЫЧАЖНЫХ МЕХАНИЗМОВ

4.1. Задачи синтеза механизмов

Наибольший интерес для конструктора представляет задача синтеза механизмов. Под синтезом понимается проектирование механизма. Синтез представляет задачу, обратную анализу, и, как все обратные задачи, сложен. В синтезе нет таких простых общих методов, какие были изучены в анализе. Многие задачи синтеза еще требуют решения.

Различают три стадии синтеза рычажных механизмов. Первая стадия – синтез структурной схемы. Он относительно прост и сводится к выбору механизма, удовлетворяющего общим требованиям к нему. На этой стадии изучаются аналоги данного механизма, используется справочная литература (например, семитомный справочник «Механизмы в современной технике» под ред. И.И. Артоболевского, «Механизмы» под ред. С.Н. Кожевникова, «Словарь-справочник по механизмам» А.Ф. Крайнева).

Вторая стадия – метрический синтез. Здесь определяются размеры звеньев механизма, при которых удовлетворяются поставленные требования. Метрический синтез опирается на приемы кинематического анализа, так что зачастую синтез сводится к многократному повторению анализа.

Третья стадия – динамический синтез. Это наиболее общая задача синтеза, в которой учитываются не только кинематические, но и динамические требования к механизму.

Ввиду сложности задач синтеза ограничимся изложением частных случаев, имеющих простое, в основном геометрическое решение. Задачи такого рода в инженерной практике встречаются довольно часто. Подавляющее большинство применяемых рычажных механизмов представляют разновидности четырехзвенных механизмов, поэтому остановимся в основном на них.

4.2. Структурный синтез рычажных механизмов

Изучая модель шарнирного четырехзвенника, можно обнаружить, что в зависимости от того, какое звено принято за неподвижное, а какое – за входное, изменяются основные свойства механизма: механизм может быть кривошипно-коромысловым, двухкривошипным, двухкоромысловым. Наибольшее применение находит кривошипно-коромысловый механизм.

Выясним условия существования кривошипа. Для этого следует рассмотреть механизм в крайних положениях. Крайним положением механизма называют такое, при котором ведомое звено занимает крайнее положение. Механизм имеет два крайних положения. Признак крайнего положения в кривошипно-коромысловом механизме – кривошип и шатун располагаются на одной линии (рис. 4.1,а). В двухкоромысловом механизме в крайних положениях шатун и коромысло располагаются на одной линии (рис. 4.1,б).

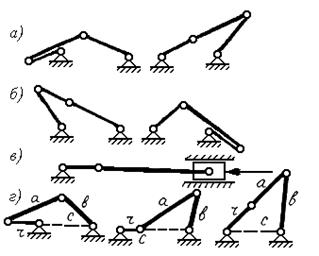
Рис. 4.1.Особые положения шарнирного четырехзвенника:

а-крайние положения кривошипно-коромыслового механизма, б- крайние положения двухкоромыслового механизма, в –мертвое положение, г – условие существования кривошипа

«Мертвым» называется положение, при котором возникает неопределенность движения ведомого звена (рис. 4.1,в). Для выхода из «мертвого» положения необходимо «подтолкнуть» ведомое звено, например силами инерции маховика.

Существование кривошипа – это его возможность повернуться вокруг центра вращения на 360˚. Наиболее опасными в этом отношении являются положения, в которых кривошип и стойка лежат на одной линии (рис. 4.1,г). Там же представлено еще одно дополнительное положение. Исходя из свойств длин сторон треугольника, можно записать неравенства:

r + c < a + b; b <c – r + a; r + b <c + a; r + a <b + c.

Складывая первое со вторым, второе с третьим и первое с третьим неравенства, получим

r < a; r < c; r < b.

Отсюда следует, что для существования кривошипа необходимо соблюдать условия:

- кривошип есть наименьшее звено.

- сумма длин наименьшего и наибольшего звеньев меньше суммы длин двух других звеньев (эти условия известны как теорема Грасгофа).

Если в кривошипно-коромысловом механизме сделать стойкой наименьшее звено, то получится двухкривошипный механизм, а если сделать стойкой звено противоположное наименьшему – то двухкоромысловый (рис. 4.2,а).

Если в шарнирном четырехзвеннике длины звеньев попарно равны (r = b, a = c), то получится шарнирный параллелограмм (рис. 4.2,б). Это

двухкривошипный механизм, у которого шатун движется поступательно. Он находит применение, например, в качестве спарника колес тепловоза, входит в состав пантографов. В другой сборке получается шарнирный антипараллелограмм.

Рис. 4.2 Варианты четырехзвенных механизмов:

а –двухкривошипный и двухкоромысловый, б –шарнирный параллелограмм и антипараллелограмм, в – механизм Галловея,

г – кривошипно-ползунный механизм, д – кулисные механизмы

Если r = c, a = b = 2r, получается двухкривошипный механизм Галловея, у которого за один оборот кривошипа b кривошип r делает два оборота (рис.4.2,в). Если коромысло кривошипно-коромыслового механизма сделать бесконечно большим, траектория точки В будет представлять прямую линию. Механизм превратится в кривошипно-ползунный (рис.4.2,г).

Принимая за стойку различные звенья кривошипно-ползунного механизма, получим другие механизмы, Если длина кривошипа больше длины стойки, получим механизм с вращающейся кулисой, если длина кривошипа меньше длины стойки – механизм с качающейся кулисой (рис. 4.2,д). Если их длины равны – за каждые два оборота кривошипа кулиса совершает один оборот. Кулисные механизмы с качающейся кулисой применяются для получения медленного рабочего хода и быстрого холостого хода.

4.3. Синтез четырехзвенных механизмов по заданным

положениям звеньев

Требуется спроектировать кривошипно-коромысловый механизм, у которого коромысло занимает два заданных крайних положения, или, иными словами, задан размах колебания коромысла ψ. Выберем центр вращения кривошипа -точку О. Зададимся произвольными значениями длины кривошипа r и длины шатуна a (рис. 4.3,а). Тогда в левом крайнем положении

a - r = OB₁.

В правом крайнем положении

a + r = OB₂ .

Отрезки ОВ₁ и ОВ₂ можно замерить на чертеже. Имеем два линейных уравнения относительно r и a, решения которых находятся элементарно:

r = (OB₂ - OB₁) /2; (4.1)

a = (OB_{2 +} OB₁)/2.

Поскольку точка О выбрана произвольно, задача имеет бесконечное множество решений.

Рис. 4.3 Синтез четырехзвенных механизмов:

а –по заданным положениям коромысла,

б – по заданным положениям ползуна, по заданным положениям шатуна

Аналогичным образом можно спроектировать кривошипно-ползунный механизм по заданным положениям ползуна. Для центрального механизма из формул (4.1) следует

r = H / 2,

где H - ход ползуна.

Пусть требуется спроектировать механизм, у которого шатун занимает два произвольных заданных положения (рис. 4.3,в) Соединим точки А₁ и А₂, В₁ и В₂ отрезками прямых, в серединах их восстановим перпендикуляры. На этих перпендикулярах выберем точки О и С. Приняв их за центры вращения кривошип,а и коромысла, построим механизм, у которого точки А и В, двигаясь по дугам А₁А₂ и В₁В₂, попадут в точки А₂ и В₂. Задача имеет бесконечное множество решений. Таким путем можно спроектировать различные опрокидыватели, перегружатели и т.д.

В отличие от рассмотренной выше задачи проектирование механизма по заданным положениям шатуна имеет единственное решение. Центры вращения кривошипа и коромысла находятся в точках пересечения соответствующих перпендикуляров.

4.4. Синтез механизмов по коэффициенту производительности

Коэффициентом производительности циклового механизма называется отношение средней скорости холостого хода к средней скорости рабочего хода. Название объясняется тем, что соотношение этих скоростей влияет на производительность машины, в которой используется такой механизм.

k = V_x / V_p .

Выразим k через геометрические параметры механизма:

k = V_x / V_p = φ_p / φ_x . (4.2)

Здесь использованы соотношения:

V_x = S / tx; Vp = S / tp; tp = φ_p / ω; t_x = φ_x ω,

где φ_{р и} φ_х - углы поворота кривошипа, соответствующие рабочему и холостому ходу ведомого звена; ω - скорость вращения кривошипа.

Коэффициент производительности для кулисных механизмов обычно находится в пределах 1.5 - 2.0

Построим кулисный механизм в двух крайних положениях (рис. 4.4,а) В крайних положениях кривошип перпендикулярен кулисе. Полный угол поворота кривошипа, соответствующий циклу работы механизма, состоит из угла рабочего хода φ_р и угла холостого хода φ_х. Так как требуется k > 1, φ_р принимается большим из двух углов между положениями кривошипа в крайних положениях механизма. Из построений на рис. 4.4,а нетрудно увидеть, что

φ_p = 180˚ + ψ;

φ_x = 180˚ - ψ,

где ψ – угол между OA₂ и OA₁ - угол размаха (качания) кулисы.

Подставив значения φ_р и φ_х в (4.2), получим

k = (180˚ + ψ) / (180˚ - ψ).

Откуда следует:

ψ = 180˚ (k – 1) / (k+1). (4.3)

Радиус кривошипа найдем, рассмотрев треугольник ОА₁С:

r = c sin (ψ /2),

где С – длина стойки ОС.

В механизме на рис. 4.4,б, включающем механизм с вращающейся кулисой, крайние положения определяются присоединенной группой, представляющей центральный кривошипно-ползунный механизм. Изобразив его в крайних положениях, найдем соответствующие положения кривошипа ОА₁ и ОА₂ и углы φ_р и φ_х. Из треугольника ОАС следует:

r = c / sin (ψ /2),

где с – длина стойки ОС.

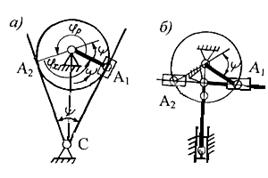
Рис. 4.4 К синтезу рычажных механизмов с качающейся и

вращающейся кулисой

4.5. Учет угла давления при синтезе механизмов

Углом давления θ называется угол между направлением силы и направлением перемещения, вызванного этой силой. Углом передачи μ называется угол, дополняющий угол давления до 90˚.

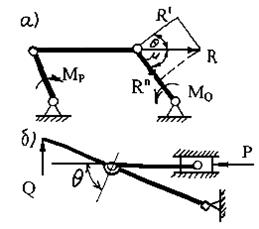
Рис. 4.5 К понятию угла давления в рычажном механизме

На рис. 4.5,а указаны углы давления и угол передачи в точке В шарнирного четырехзвенника. Разложим силу на нормальную и касательную составляющие. Чем больше угол давления, тем меньше составляющая Rⁿ и больше составляющая R^τ. Полезно используется только составляющая R^τ, а составляющая Rⁿ создает трение в кинематических парах. Следовательно, чем меньше угол давления, тем выше к.п.д. Наилучший случай, когда угол давления равен нулю. Однако по характеру работы механизма этот угол не может оставаться постоянным. В шарнирных механизмах угол давления допускается до 45˚, в механизмах с поступательными парами – до 30˚. В ответственных механизмах, таких как кривошипно-ползунный механизм

двигателя внутреннего сгорания, угол давления принимается еще меньше – до 15˚. На рис. 4.5,б представлен пример неудачно спроектированного механизма обжима борта в станке для сборки автомобильных шин на предприятии «Беларусьшина». Здесь угол давления принят слишком большим. В результате для преодоления полезной нагрузки необходимо прилагать очень большое усилие.

4.6. Направляющие механизмы. Механизмы с выстоями

Направляющие рычажные механизмы предназначены для осуществления движения исполнительной точки по заданной траектории. В отличие от них передаточные механизмы служат для преобразования параметров движения или усилий. Известно большое количество рычажных механизмов, служащих для построения графиков простейших функций. Сведения о них можно найти в справочниках (В.А.Юдин «Механизмы приборов»). С помощью таких механизмов можно построить очень сложные кривые, например, аэродинамический профиль.

В том случае, если нельзя найти готовой схемы, можно воспользоваться следующим методом синтеза механизма, приближенно воспроизводящего заданную кривую. Выберем произвольную точку О, кривошип и шатун (рис. 4.6). Свяжем с шатуном планшет с нанесенными на ней чертящими точками. Осуществляя движение точки М планшета по заданной траектории, построим траектории остальных чертящих точек. Выберем из них наиболее приближающуюся к окружности. Найдем ее центр и поместим в него шарнир С. Соединив чертящую точку В с точкой А и точкой С, получим шарнирный четырехзвенник, у которого точка М шатуна будет приближенно воспроизводить заданную кривую.

Среди многих механизмов, созданных П.Л.Чебышевым, широко известны прямолинейно направляющий («лямбдообразный») и круговой направляющий механизмы. На их основе можно создать механизмы с выстоями.

Механизмом с выстоем называется такой механизм, в котором при непрерывном движении ведущего звена ведомое звено часть времени неподвижно. На рис. 4.6,б представлены две схемы механизмов с выстоями, основанные на механизмах Чебышева. Механизмы с выстоями

применяются в различных машинах – автоматах.

Мгновенный выстой называется остановкой. Механизмы с остановками применяются с целью улучшения динамики процесса.

Не нашли, что искали? Воспользуйтесь поиском: