Sin ψ1 cos ψ1 sin2 α / (1 – sin2ψ1 sin2α))ω3 ω1 .

Рис. 4.13. Образование четырехзвенного сферического механизма

Иногда эти уравнения записываются немного иначе, но это объясняется другим выбором осей, относительно которых указываются углы.

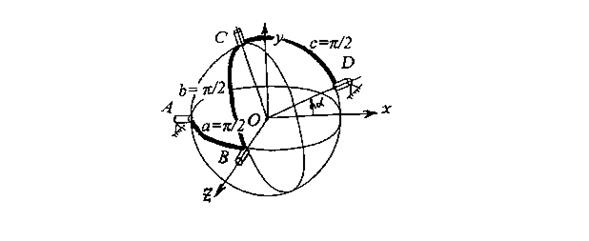
Рис.4.14. Четырехзвенный сферический механизм -шарнир Гука

Из анализа этих уравнений вытекает, что при равномерном вращении входного вала вращение выходного вала будет периодически неравномерным, эта неравномерность тем больше, чем больше угол α.

В случае, когда угол α = 90˚, при равномерном вращении входного вала выходной вал осуществляет качательное движение. Механизм получил название прямой ключ Гука. Его другое название – механизм косой шайбы. Наиболее известное примнение этого механизма - в сельхозмашинах, для привода ножей косилки. Основное уравнение для этого механизма

tg ψ₃ = tg (β – π / 2) cos ψ_1,

где угол β – угол между осями шарниров А и В (в шарнире Гука он равен 90˚).

Рассмотренный выше шарнир Гука относится к асинхронным карданам. В то же время в автомобилях с передним приводом используются синхронные карданы, т.е. механизмы, обеспечивающие равномерное вращение выходного вала при любом угле между валами. Среди большого количества таких механизмов наиболее интересен универсальный кардан Рзеппа. Он применяется в большинстве современных переднеприводных легковых автомобилей в передаче движения от двигателя к ведущим колесам. Его техническое название – шарнир равных угловых скоростей (ШРУС) (Рис. 4.15).

Кардан Рзеппа обеспечивает передачу вращения со строго постоянной угловой скоростью.Механизм чрезвычайно остроумный и его принцип действия требует особого обьяснения.

Связь входного и выходного валов осуществляется посредством шариков.Если бы шарики были зафиксированы относительно одного из валов, то это был бы кардан типа шарнира Гука. В кардане Рзеппа постоянная угловая скорость обеспечивается за счет того, что шарики принудительно устанавливаются в биссектральную плоскость угла между входным и выходным валом между входным и выходным валом. Это происходит благодаря смещению кановок внутренней втулки и вилки относительно оси и криволинейностью их в меридиональной плоскости. Центры этих канавок симметрично расположены относительно центра шарнира. Шарики удерживаются в плоскости постоянной частоты вращения специальной обоймой. Контактирующие поверхности обоймы и внутренней и внешней втулок выполнены сферическим с общим центром в точке О. Принудительное перемещение шариков в биссектральную плоскость осуществляется за счет специального выполнения канавок на втулках.

Рис.4.15. Синхронный кардан Рзеппа

Принцип обеспечения передачи вращения со строго постоянной частотой поясняется рисунком 4.15,б. Здесь требуется доказать, что линия x - x′ располагается

в биссектральной плоскости угла AOA′, образованного осями входного и выходного валов.

Центр шарика располагается в точке S. Угол θ – угол между осями валов. Точки А и А′ - центры окружностей канавок внешней и внутренней втулок, установленных соответственно на выходном и входном валах. Эти центры расположены на одинаковых расстояниях от общего центра шарнира – точки О.

Канавки на втулках определяют единственно возможное положение шарика. При любом положении осей центр шарика располагается в точке пересечения радиусов R, проведенных из центров окружностей канавок. Поскольку треугольники ОАS и ОА′S равны, ось x-x′ располагается в биссектральной плоскости.

Контрольные вопросы

1. В чём состоят и как решаются задачи синтеза механизмов?

2. Что такое структурный синтез, кинематический и динамический синтез?

3. Какие механизмы можно получить преобразованием размеров из шарнирного четырёхзвенника?

4. Что такое коэффициент производительности циклового механизма?

5. Какое значение для работы механизма имеет угол давления?

6. Приведите примеры шаговых механизмов.

7. Какими особенностями обладают механизмы пантографов?

5. СИНТЕЗ ЗУБЧАТЫХ МЕХАНИЗМОВ

5.1. Классификация зубчатых механизмов

Зубчатые механизмы – это самый распространенный и пожалуй самый важный вид механизмов. Трудно найти такую машину, в которой нет зубчатого механизма. Они применяются в станках, в грузоподъемных машинах, автомобилях, разнообразных технологических машинах и т.д. Основные достоинства зубчатых механизмов, определившие их широкое применение, - строго постоянное передаточное отношение, большая передаваемая мощность на единицу массы, компактность, долговечность, высокий к.п.д. Недостаток – сложность изготовления и высокая стоимость.

Рис. 5.1. Зубчатая передача

Зубчатые механизмы предназначены для передачи вращательного движения и преобразования его параметров. Обычно двигатели обладают скоростью и моментом, как правило, не подходящим для использования в технологическом процессе. Преобразование параметров вращательного движения возможно посредством прижатых друг к другу гладких дисков (рис. 5.1), образующих фрикционные передачи. Ее недостаток – ограниченная мощность из-за большой нагрузки на подшипники, неизбежное проскальзывание, износ поверхностей, потери мощности. Практически передаваемая мощность в таких механизмах не превышает 10 – 20 квт.

Чтобы устранить отмеченные недостатки, диски снабжаются чередующимися выступами и впадинами, располагающимися с определенным интервалом. Такие выступы называются зубьями.

Зубчатым колесом называется звено с замкнутой системой зубьев, обеспечивающей непрерывность движения. Различают еще зубчатый сектор, зубчатую рейку.

Зубчатая передача – трехзвенный механизм, состоящий из двух колес и стойки.

Важнейшей характеристикой зубчатой передачи является передаточное отношение – отношение угловых скоростей колес.

Две или более зубчатые передачи образуют зубчатый механизм.

Зубчатые колеса, зубчатые передачи и зубчатые механизмы чрезвычайно разнообразны. Поэтому целесообразно ознакомиться с их простейшей классификацией.

Зубчатые колеса бывают:

а) цилиндрические и конические,

б) прямозубые, винтовые, шевронные,

в) эвольвентные, циклоидальные, цевочные, трохоидальные, круговинтовые,

г) с внешним и с внутренним зацеплением.

Винтовые колеса могут быть с левым и с правым наклоном зуба. Винтовые колеса с винтовой линией постоянного шага называют косозубыми.

Зубчатые передачи бывают:

а) с постоянным и переменным передаточным отношением некруглые колеса),

б) плоские и пространственные,

в) с параллельными, пересекающимися и скрещивающимися осями колес.

По этому признаку различают цилиндрические, конические, гиперболоидные передачи.

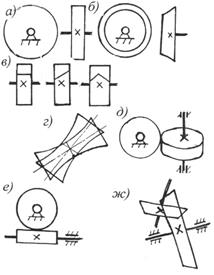
Рис. 5.2. Виды зубчатых колес и зубчатых передач

В гиперболоидных передачах звенья выполняются в форме гиперболоида вращения. Гиперболоид – линейчатая поверхность, образуемая при вращении произвольно расположенной в пространстве прямой линии относительно некоторой оси. Таким образом, образующей поверхности гиперболоида является прямая линия. Два сопряженных гиперболоида перекатываются друг по другу без скольжения и касаются по прямой линии. Если их снабдить зубьями, образуется точная гиперболоидная передача (рис. 5.2,г). На практике используется приближенная гиперболоидная передача, образованная из цилиндрических и конических колес. В таком случае касание их происходит не по линии, а в точке. Частными случаями гипоидной передачи служат винтовые (рис.5.2,д), червячные (рис. 5.2,е) и гипоидные передачи (рис. 5.2,ж).

Различают также понижающие и повышающие частоту вращения передачи (редукторы и мультипликаторы), передачи внешнего, внутреннего зацепления, реечные передачи.

Зубчатые механизмы бывают: а) с неподвижными осями колес (рядовые) и с подвижными осями (планетарные), б) механизмы предназначенные для передачи большой мощности (силовые) и для преобразования параметров движения (кинематические), в) механизмы с одной степенью подвижности и зубчатые дифференциалы.

5.2. Понятие о центроидных механизмах

Зубчатые механизмы относятся к разряду центроидных механизмов, в основе образования которых лежит центроида. Из теоретической механики известно, что мгновенное плоское движение твердого тела можно привести к одному мгновенному вращению вокруг оси, точка пересечения подвижной центроиды по неподвижной, причем подвижная центроида считается жестко связанной с твердым телом, а неподвижная – с системой отсчета. Таким образом, любое плоское движение можно осуществить, подобрав надлежащие центроиды. Сказанное хорошо иллюстрируется на модели шарнирного антипараллелограмма. В этом случае центроидами являются эллипсы (рис.5.3). Снабдив их зубьями, получим эллиптическую зубчатую передачу, в которой при равномерном движении ведущего звена ведомое вращается неравномерно. Такие передачи используются, например, в текстильных машинах.

Рис. 5.3. Центроиды зубчатых колес

5.3. Основной закон зацепления

Простейшие зубчатые механизмы применялись еще в древнейшие времена, например, для передачи движения с водяного колеса на жернов. Профиль зубьев мог быть любым, выдерживался только постоянный шаг. Увеличение быстроходности передачи потребовало соответствующего профилирования зубьев. при случайном выборе профиля зубьев мгновенное передаточное отношение переменно, что недопустимо, т. к. колебания скорости выходного звена вызывают инерционные нагрузки, удары в передаче. Профиль зубьев должен быть таким, чтобы угловая скорость выходного звена была строго постоянной.

Рис. 5.4. Зацепление двух профилей

Чтобы ответить на вопрос, каким должен быть профиль, вначале познакомимся с основным законом зацепления.

Нормаль, проведенная через точку касания двух профилей, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям этих профилей.

Требуется доказать, что O₁P / O₂ P =ω₂ / ω₁ (рис.5.4)

Через точку А проведем нормаль N – N и касательную Т – Т и разложим скорости точек А₁ и А₂ на эти направления. Заметим, что v₁ = ω₁ r_1, v₂ = ω₂ r₂. Кроме того, v₁ⁿ = v₂ⁿ - из условия отсутствия вдавливания профилей или их размыкания. Тангенциальные составляющие v₁^τ ≠ v₂^τ, что

обусловливает скольжение профилей. Из подобия треугольников AV₁V₁ⁿ и O₁B₁A следует:

V₁ⁿ/V₁ = r_b1 / r₁

откуда V₁ⁿ = ω₁ r_b1. Из подобия треугольников AV₂V₂ⁿ и O₂B₂A следует: V₂ⁿ / V₂ = r_b2 / r₂

откуда V₂ⁿ = ω₂ r_b2. Учитывая, что V₁ⁿ = V₂ⁿ, получим ω₁ r_b1 = ω₂ r_b2.

Из подобия треугольников O₁B₁P и O₂B₂P следует r_b1 / r_b2 = O₁P / O₂P. С учетом записанных выше соотношений получим ω₁ / ω₂ = O₂P / O₁P, что и требовалось доказать.

Следствие основного закона зацепления: для постоянства передаточного отношения необходимо, чтобы нормаль, проведенная через точку касания двух профилей, пересекала межосевую линию в постоянной точке (полюсе зацепления). Иными словами требуется неизменность положения полюса.

В качестве профилей зубьев могут использоваться кривые, для которых выполняется указанное требование, Такие кривые называются сопряженными. К ним, в частности, относится эвольвента окружности.

5.4. Эвольвента окружности. Построение и свойства

Геометрическое место центров кривизны какой-либо кривой называют эволютой, а саму кривую – эвольвентой (рис. 5.5). При профилировании зубьев в качестве эволюты используется окружность, называемая в дальнейшем основной, а сам зуб очерчивается эвольвентой окружности. Единственным параметром, отличающим одну эвольвенту от другой, является радиус основной окружности.

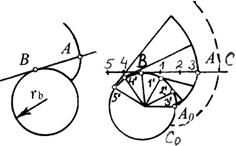
Рис. 5.5. Образование эвольвенты

Можно указать следующий способ образования эвольвенты. Выбирается основная окружность радиуса r_{b ,} касающаяся ее производящая прямая АВ и чертящая точка на ней. Перекатывая производящую прямую по окружности без скольжения, получаем траекторию чертящей точки, которая является эвольвентой, т.к. мгновенные радиусы кривизны ее лежат на основной окружности. Эвольвенту можно получить, наматывая нить с чертящей точкой на диск (рис. 5.5). Две чертящие точки дадут две эквидистантные (равноотстоящие) эвольвенты.

Приближенное графическое построение эвольвенты как кривой, составленной из множества дуг окружностей, представлено на рис.5.5 б.

Из определения эвольвенты и из указанных выше способов ее построения вытекают следующие очевидные свойства:

1. Нормаль эвольвенты касается основной окружности.

2. Радиус кривизны эвольвенты равен длине нормали.

3. Длина нормали эвольвенты равна длине соответствующей дуги основной окружности

4. Расстояние между эквидистантными эвольвентами равно длине соответствующей дуги основной окружности.

5.5. Уравнение эвольвенты в полярных координатах

Наиболее удобная форма записи уравнения эвольвенты – в полярных координатах в параметрической форме. В качестве параметра принимается угол профиля эвольвенты. Углом профиля эвольвенты α_y называется угол между направлением радиус–вектора к текущей точке Y и направлением касательной Т – Т. Он изменяется в пределах 0 - 90˚, практически используется участок эвольвенты, где α_y = 0 - 30˚.

Рис. 5.6. К выводу уравнения эвольвенты

Полярные координаты r_y и θ_y укажут положение точки Y. Установим зависимость r_y и θ_y от параметра α_{y .}

Проведем из точки Y нормаль N –N, которая по 1-му свойству эвольвенты коснется основной окружности в точке В. Заметим, что угол BOY равен углу профиля эвольвенты в данной точке. Из треугольника OBY следует

r_y = r_b / cos α_y.

Введем угол ν_{y ,} тогда ν_y = α_y + θ_y, откуда следует θ_y = ν_y - α_y.

Из построений на рис. 5.6 и в силу 3-го свойства эвольвенты длина дуги ВА₀ равна BY. Из треугольника BYO следует BY/r_b = tg α_{y .} На основании приведенных зависимостей нетрудно установить, что центральный угол ν_y = tg α_y. Функция θ_y = tg α_y - α_y получила название эвольвентной функции или инволюты. Иногда используется условное обозначение θ_y = - inv α_y.

5.6. Эвольвентное зацепление

На рис. 5.7 представлено зацепление эвольвентных профилей. Общая нормаль N – N. Проведенная через точку касания двух профилей, обязана согласно 1-му свойству эвольвенты, коснуться основных окружностей. Поскольку таких окружностей две, положение нормали единственно и неизменно. Тем самым подтверждается выполнение следствия основного закона зацепления. В процессе зацепления точка касания профилей не может сойти с общей нормали N – N, т.к. в противном случае нарушилось бы 1-ое свойство. Установлено, что при эвольвентном зацеплении профилей точка касания движется по общей нормали с постоянной скоростью.

Введем две окружности, проходящие через полюс зацепления. Такие окружности называются начальными. Они перекатываются друг по другу без скольжения и служат центроидами зубчатых колес.

Рис. 5.7. Эвольвентное зацепление

Эвольвентное зацепление нечувствительно к небольшому изменению межосевого расстояния, что удешевляет изготовление корпусных деталей.

1. Для нарезания эвольвентных зубчатых колес можно применять простой инструмент с прямолинейной режущей кромкой.

2. При изготовлении колес путем простого смещения инструмента можно добиваться новых положительных свойств.

5.7. Изготовление зубчатых колес

Существуют два способа изготовления зубчатых колес: способ копирования и способ обкатки. Способом копирования дисковой или пальцевой фрезой на обычном фрезерном станке вырезается впадина между зубьями (рис.5.8). Поскольку в зависимости от числа зубьев размеры впадины при одном и том же модуле изменяются, нужно иметь очень много фрез. На практике одной фрезой нарезаются колеса в некотором диапазоне чисел зубьев, указанном на фрезе, что не очень точно. Неточность может быть исправлена последующей шлифовкой.

Рис. 5.8. Два способа изготовления зубчатых колес:

способ копирования –а, способ обкатки –б

Способ копирования недостаточно производителен, т.к. в работе находится один зуб, много времени тратится на перестановку заготовки. Поэтому способ применяется в единичном и мелкосерийном производстве, при нарезании неответственных, тихоходных колес.

При способе обкатки инструмент и заготовка совершают относительное движение обкатывания. Инструмент своими режущими кромками постепенно внедряется в заготовку, прокладывая себе путь. Таким образом, возникает станочное зацепление, аналогичное обычному зацеплению с той разницей, что одно из звеньев является инструментом. Инструмент выполняется в виде гребенки, червячной фрезы или долбяка. Этот способ требует применения специальных зубофрезерных станков. В одних конструкциях станков инструмент обкатывается вокруг неподвижной заготовки, в других – инструмент движется поступательно, заготовка поворачивается, в третьих – заготовка и инструмент (долбяк) вращаются (рис.5.8).

Способ обкатки получил наибольшее распространение. Он производителен, т.к. обрабатывается несколько зубьев сразу, процесс зубонарезания идет непрерывно. Профиль зуба формируется с учетом числа зубьев колеса, поэтому нарезание точное. По такому же принципу производится чистовая обработка, шлифование зубьев.

5.8. Исходный контур

Из описания способов изготовления зубчатых колес ясно, что размеры зуба полностью зависят от профиля инструмента. По ГОСТ профиль инструмента стандартизован путем задания так называемого «исходного контура». На рис.5.9,а представлен теоретический исходный контур. Он выполнен в виде рейки с трапециевидными зубьями.

Размеры рейки выражаются через один основной параметр, называемый модулем. Модуль m имеет размерность мм и выбирается из ряда рациональных чисел от 0.05 до 100.

Рис. 5.9 Теоретический и производящиий исходный контур

Не нашли, что искали? Воспользуйтесь поиском: